Symmetrische Funktionen: Die elegante Welt gerader Funktionen
Spiegelsymmetrie – ein faszinierendes Konzept, das nicht nur in der Kunst und Architektur, sondern auch in der Mathematik eine wichtige Rolle spielt. Welche Funktionen spiegeln diese Symmetrie wider? Die Antwort: Gerade Funktionen. Aber wann genau ist eine Funktion gerade?
In diesem Artikel tauchen wir ein in die Welt der geraden Funktionen und erkunden ihre Eigenschaften, ihre Bedeutung und ihre Anwendungsmöglichkeiten. Von der grundlegenden Definition bis hin zu praktischen Beispielen und Tipps – wir beleuchten alle Aspekte dieses spannenden mathematischen Konzepts. Bereiten Sie sich darauf vor, die Eleganz und Symmetrie gerader Funktionen zu entdecken!
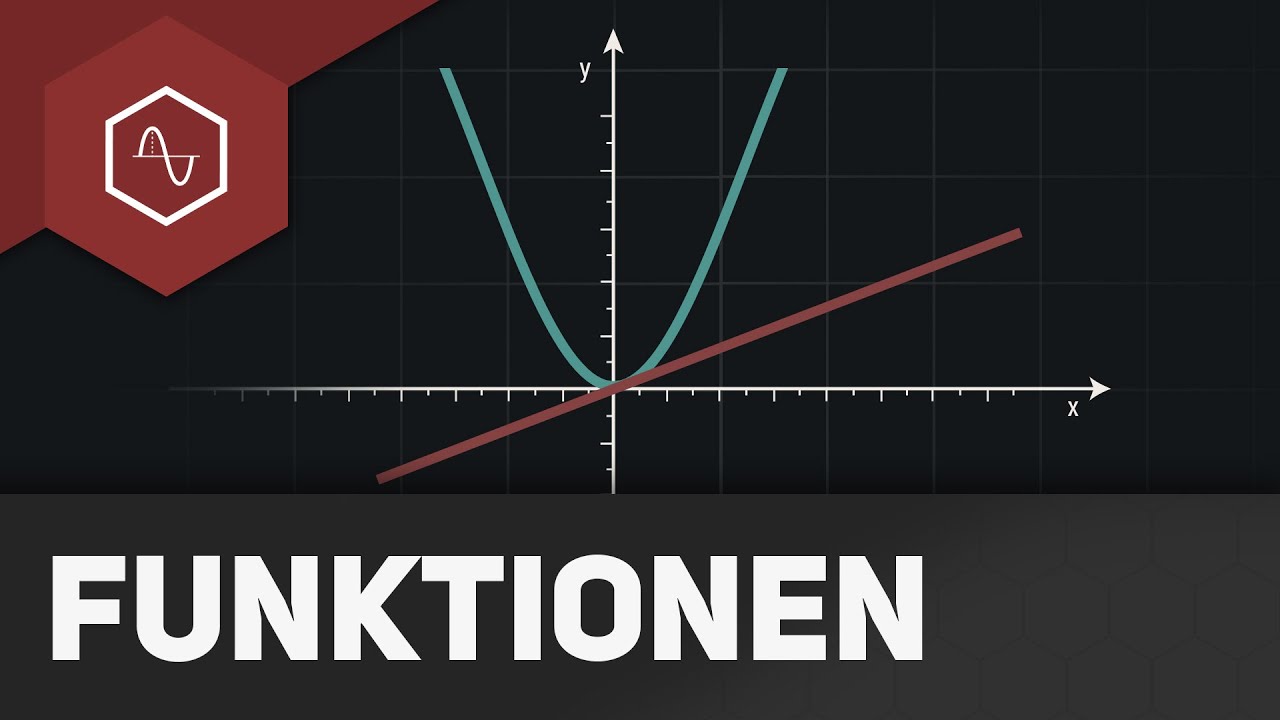
Die Frage "Wann ist eine Funktion gerade?" ist fundamental für das Verständnis dieses mathematischen Prinzips. Eine Funktion gilt als gerade, wenn ihr Graph symmetrisch zur y-Achse ist. Das bedeutet, für jeden x-Wert gilt: f(x) = f(-x). Anders ausgedrückt: Egal ob wir einen positiven oder den entsprechenden negativen x-Wert einsetzen, das Ergebnis der Funktion bleibt gleich.
Die Symmetrie gerader Funktionen hat weitreichende Konsequenzen für ihre Eigenschaften. So vereinfacht sich beispielsweise die Berechnung von Integralen über einen symmetrischen Bereich erheblich. Auch in der Physik und anderen Naturwissenschaften spielen gerade Funktionen eine wichtige Rolle, da sie häufig natürliche Phänomene beschreiben, die eine inhärente Symmetrie aufweisen.
Das Konzept der geraden Funktionen hat seine Wurzeln in der klassischen Analysis. Schon früh erkannten Mathematiker die Bedeutung der Symmetrie zur y-Achse und entwickelten die entsprechenden Definitionen und Rechenregeln. Die Untersuchung gerader Funktionen ist eng verbunden mit der Entwicklung der Trigonometrie und der Fourier-Analyse, die wiederum wichtige Werkzeuge für die Beschreibung periodischer Phänomene darstellen.
Ein einfaches Beispiel für eine gerade Funktion ist f(x) = x². Egal ob wir x = 2 oder x = -2 einsetzen, das Ergebnis ist immer 4. Der Graph dieser Funktion, eine Parabel, ist symmetrisch zur y-Achse. Weitere Beispiele sind die Kosinusfunktion cos(x) und die Absolutwertfunktion |x|.
Vorteile gerader Funktionen:
1. Vereinfachte Integration: Die Symmetrie erleichtert die Berechnung von Integralen.
2. Vereinfachte Darstellung: Gerade Funktionen lassen sich oft durch einfachere Formeln darstellen.
3. Verständnis von Symmetrien: Sie helfen, Symmetrien in physikalischen und anderen Systemen zu verstehen.
Häufig gestellte Fragen:
1. Was ist der Unterschied zwischen einer geraden und einer ungeraden Funktion?
2. Wie kann man grafisch überprüfen, ob eine Funktion gerade ist?
3. Gibt es Funktionen, die weder gerade noch ungerade sind?
4. Welche Rolle spielen gerade Funktionen in der Physik?
5. Wie berechnet man die Ableitung einer geraden Funktion?
6. Wie findet man die Nullstellen einer geraden Funktion?
7. Wie kann man eine gerade Funktion konstruieren?
8. Welche Bedeutung haben gerade Funktionen in der Signalverarbeitung?
Tipps und Tricks: Um schnell zu überprüfen, ob eine Funktion gerade ist, ersetzen Sie x durch -x. Wenn die resultierende Funktion identisch mit der ursprünglichen Funktion ist, ist die Funktion gerade.
Zusammenfassend lässt sich sagen, dass gerade Funktionen ein wichtiges Konzept in der Mathematik sind. Sie zeichnen sich durch ihre Symmetrie zur y-Achse aus und bieten zahlreiche Vorteile bei der Berechnung von Integralen und der Beschreibung symmetrischer Phänomene. Das Verständnis von geraden Funktionen ist essentiell für das Studium der Analysis, der Physik und anderer Naturwissenschaften. Nutzen Sie die hier vorgestellten Tipps und Tricks, um Ihr Wissen über gerade Funktionen zu vertiefen und ihre Eleganz in Ihren mathematischen Arbeiten zu nutzen. Die Welt der Mathematik ist voller faszinierender Entdeckungen - tauchen Sie ein und lassen Sie sich von der Symmetrie der geraden Funktionen begeistern!
Schlechtes wetter bilder lustig
Nutella vs schokolade der susse showdown
Erfolg trotz leute haben angst vor mir