Trigonometrie im Alltag Tangens einfach erklärt
Stell dir vor, du möchtest die Höhe eines Baumes berechnen, ohne ihn zu erklimmen. Oder die Steigung einer Straße bestimmen. In solchen Situationen kommt der Tangens ins Spiel, ein wichtiges Werkzeug der Trigonometrie. Dieser Artikel erklärt dir, was der Tangens (die deutsche Übersetzung von "wat is een tangens") ist und wie du ihn im Alltag anwenden kannst.
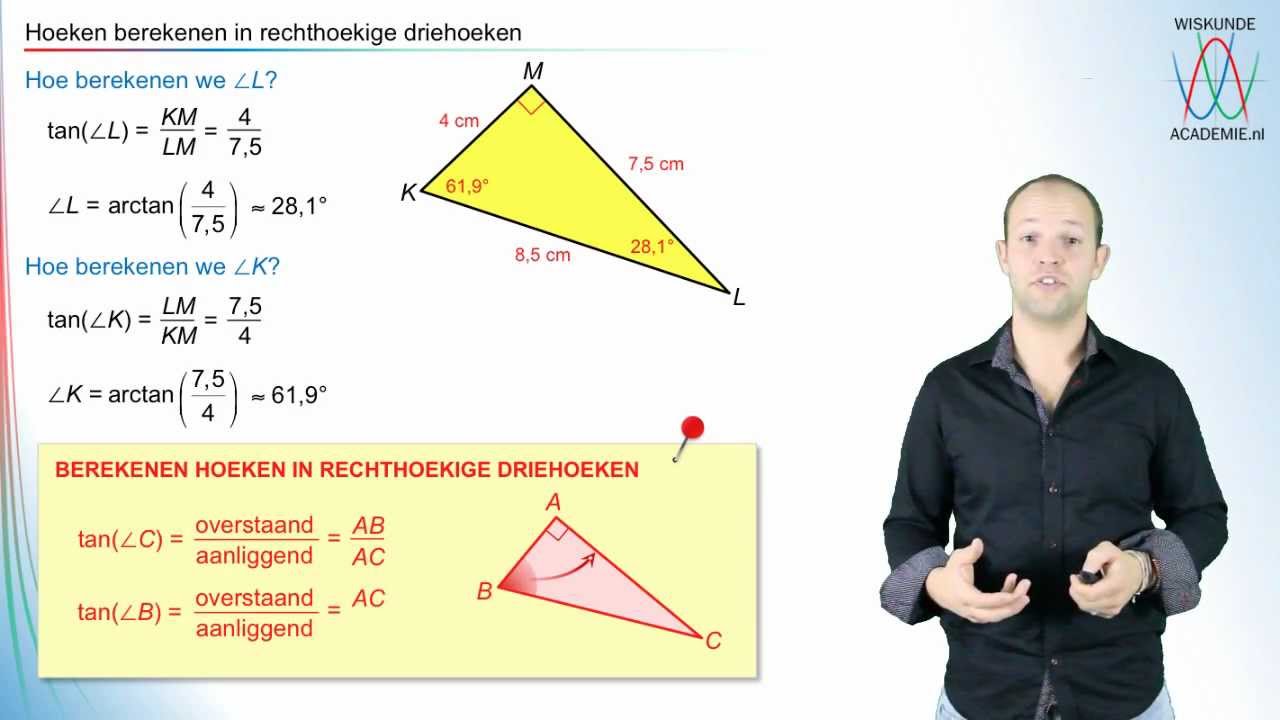
Der Tangens ist ein trigonometrisches Verhältnis, das den Zusammenhang zwischen den Seiten eines rechtwinkligen Dreiecks beschreibt. Genauer gesagt, ist der Tangens eines Winkels das Verhältnis der Länge der Gegenkathete zur Länge der Ankathete. Klingt kompliziert? Keine Sorge, wir werden das gleich mit Beispielen verdeutlichen.
Die Trigonometrie, zu der auch der Tangens gehört, hat eine lange Geschichte, die bis in die Antike zurückreicht. Schon die alten Griechen und Ägypter nutzten trigonometrische Prinzipien für astronomische Berechnungen und die Vermessung von Land. Die Entwicklung der Trigonometrie war eng mit der Entwicklung der Mathematik und Astronomie verbunden.
Die Bedeutung des Tangens liegt in seiner Fähigkeit, Winkel und Seitenverhältnisse in rechtwinkligen Dreiecken zu verknüpfen. Dies ermöglicht es uns, unbekannte Größen zu berechnen, wenn wir bestimmte Informationen über das Dreieck kennen. Die Anwendungsmöglichkeiten sind vielfältig und reichen von der Navigation und Geodäsie bis zur Physik und Ingenieurwissenschaften.
Ein häufiges Problem im Zusammenhang mit dem Tangens ist das Verständnis des Zusammenhangs zwischen Winkel, Gegenkathete und Ankathete. Es ist wichtig, sich zu merken, welcher Winkel betrachtet wird und welche Seiten die Gegenkathete und die Ankathete sind. Verwechslungen können zu falschen Ergebnissen führen.
Der Tangens eines Winkels α wird berechnet als: tan(α) = Gegenkathete / Ankathete. Beispiel: In einem rechtwinkligen Dreieck ist die Gegenkathete 4 cm lang und die Ankathete 3 cm lang. Der Tangens des Winkels α ist dann tan(α) = 4/3 ≈ 1,33.
Vorteile des Tangens:
1. Berechnung von Höhen und Entfernungen: Mit dem Tangens können wir beispielsweise die Höhe eines Turms berechnen, indem wir den Winkel zum Turmspitze und die Entfernung zum Turm messen.
2. Bestimmung von Steigungen: Der Tangens des Steigungswinkels entspricht der Steigung einer Straße oder eines Hügels.
3. Anwendungen in der Physik: Der Tangens spielt eine wichtige Rolle in der Physik, beispielsweise bei der Berechnung von Kräften und Geschwindigkeiten.
Aktionsplan zur Anwendung des Tangens: 1. Identifiziere das rechtwinklige Dreieck. 2. Bestimme den relevanten Winkel. 3. Identifiziere Gegenkathete und Ankathete. 4. Berechne den Tangens mit tan(α) = Gegenkathete / Ankathete.
Häufig gestellte Fragen:
1. Was ist der Tangens? - Das Verhältnis von Gegenkathete zu Ankathete in einem rechtwinkligen Dreieck.
2. Wie berechnet man den Tangens? - tan(α) = Gegenkathete / Ankathete.
3. Wofür wird der Tangens verwendet? - Zur Berechnung von Höhen, Entfernungen und Steigungen.
4. Was ist die Gegenkathete? - Die Seite gegenüber dem betrachteten Winkel.
5. Was ist die Ankathete? - Die Seite neben dem betrachteten Winkel, die nicht die Hypotenuse ist.
6. Was ist ein rechtwinkliges Dreieck? - Ein Dreieck mit einem 90-Grad-Winkel.
7. Wie kann ich den Tangens auf meinem Taschenrechner berechnen? - Mit der "tan"-Taste.
8. Gibt es Online-Rechner für den Tangens? - Ja, viele.
Der Tangens ist ein mächtiges Werkzeug der Trigonometrie, das uns ermöglicht, Berechnungen in rechtwinkligen Dreiecken durchzuführen. Von der Berechnung von Höhen und Entfernungen bis zur Bestimmung von Steigungen bietet der Tangens zahlreiche Anwendungsmöglichkeiten im Alltag und in verschiedenen Fachgebieten. Durch das Verständnis des Zusammenhangs zwischen Winkel, Gegenkathete und Ankathete und die Anwendung der Formel tan(α) = Gegenkathete / Ankathete können wir die Welt um uns herum besser verstehen und komplexe Probleme lösen. Nutze die Kraft des Tangens, um deine mathematischen Fähigkeiten zu erweitern und die Welt aus einer neuen Perspektive zu betrachten.
1 mai feierlichkeiten in ihrer nahe finden
E mail marketing fur kleinunternehmen dein erfolgsgeheimnis
Schafspreis was kostet ein schaf wirklich