Décryptage des Fonctions de Référence en Seconde
Le monde des mathématiques peut parfois sembler un labyrinthe complexe. Pourtant, certains concepts, comme les fonctions de référence en seconde, servent de boussoles pour naviguer dans cet univers. Mais que sont exactement ces fonctions et pourquoi sont-elles si importantes ?
Les fonctions de référence en classe de seconde constituent les fondations pour explorer des concepts plus avancés en mathématiques. Elles permettent de modéliser des situations réelles, d'analyser des données et de résoudre des problèmes concrets. Ce guide explore en profondeur ces fonctions clés, des définitions aux applications pratiques, en passant par les avantages et les difficultés qu'elles présentent.
Comprendre les fonctions de référence, c'est saisir les mécanismes fondamentaux de la variation et de la représentation graphique. De la fonction affine à la fonction carré, chaque type de fonction offre une perspective unique sur la relation entre les variables. Maîtriser ces outils mathématiques est essentiel pour progresser sereinement dans le cursus scolaire et pour développer des compétences analytiques précieuses.
L'histoire des fonctions mathématiques remonte à l'Antiquité, avec des contributions notables de mathématiciens grecs et arabes. L'étude des fonctions a évolué au fil des siècles, aboutissant à la formalisation que nous connaissons aujourd'hui. En seconde, l'accent est mis sur les fonctions de base, considérées comme des piliers pour la compréhension des concepts plus complexes abordés dans les classes supérieures.
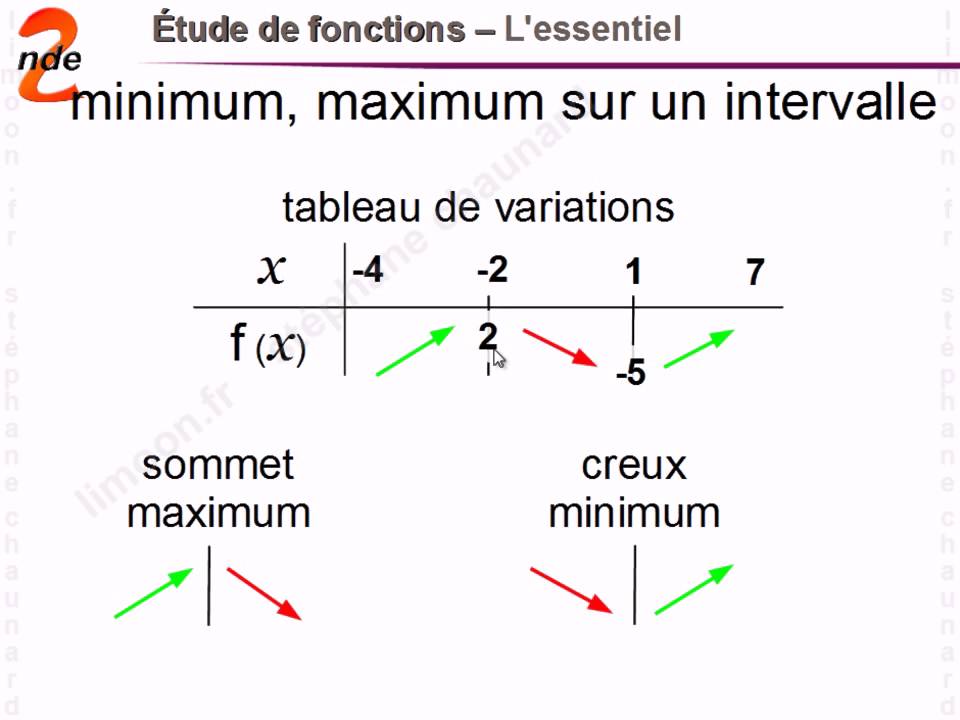
Les fonctions de référence en seconde incluent notamment la fonction affine (f(x) = ax + b), la fonction carré (f(x) = x²), et la fonction inverse (f(x) = 1/x). Chacune de ces fonctions possède des caractéristiques spécifiques, telles que leur représentation graphique, leur domaine de définition et leur sens de variation. La fonction affine représente une droite, la fonction carré une parabole, et la fonction inverse une hyperbole. Comprendre ces propriétés est crucial pour analyser et interpréter les données.
Prenons l'exemple de la fonction affine. Si a > 0, la fonction est croissante ; si a < 0, elle est décroissante. La valeur de b représente l'ordonnée à l'origine, c'est-à-dire le point où la droite coupe l'axe des ordonnées. Ces informations permettent de prédire le comportement de la fonction et de résoudre des problèmes liés à des situations linéaires.
Un autre exemple important est la fonction carré. Son graphe, une parabole, est symétrique par rapport à l'axe des ordonnées. Comprendre cette symétrie et les variations de la fonction carré est essentiel pour résoudre des équations du second degré et pour modéliser des phénomènes physiques, comme la trajectoire d'un projectile.
Les avantages de la maîtrise des fonctions de référence sont nombreux. Elles permettent de modéliser des situations réelles, de prévoir des comportements et de résoudre des problèmes concrets dans divers domaines, comme la physique, l'économie et les sciences de la vie.
Pour maîtriser les fonctions de référence, il est conseillé de s'exercer régulièrement à tracer des graphiques, à résoudre des équations et à interpréter des données. L'utilisation de logiciels de calcul formel et de ressources en ligne peut également être bénéfique.
Questions fréquemment posées :
1. Qu'est-ce qu'une fonction affine ? Une fonction affine est une fonction de la forme f(x) = ax + b.
2. Qu'est-ce qu'une fonction carré ? Une fonction carré est une fonction de la forme f(x) = x².
3. Qu'est-ce que le domaine de définition d'une fonction ? C'est l'ensemble des valeurs que peut prendre x.
4. Comment tracer le graphe d'une fonction affine ? En déterminant deux points appartenant à la droite.
5. Comment tracer le graphe d'une fonction carré ? En utilisant la symétrie et quelques points clés.
6. Comment déterminer le sens de variation d'une fonction ? En étudiant le signe du coefficient directeur pour la fonction affine, et en observant la parabole pour la fonction carré.
7. Quelles sont les applications des fonctions de référence ? Elles permettent de modéliser des situations réelles dans divers domaines.
8. Où trouver des exercices sur les fonctions de référence ? Dans les manuels scolaires, en ligne et dans des ouvrages spécialisés.
En conclusion, les fonctions de référence en seconde sont des outils mathématiques essentiels pour comprendre le monde qui nous entoure. Elles permettent de modéliser des situations, de résoudre des problèmes et de développer des compétences analytiques précieuses. Maîtriser ces fonctions est un investissement pour l'avenir, ouvrant la voie à des études supérieures et à des carrières dans des domaines variés. N'hésitez pas à approfondir vos connaissances et à pratiquer régulièrement pour consolider vos acquis et explorer toutes les potentialités offertes par ces outils mathématiques fondamentaux.
Le grand retour du foot universitaire date de sortie dea sports college football
Retour vers le futur lage dor du rocknroll
Decrochez votre reve reussir sa lettre de motivation pour un projet professionnel daide soignante