Svelata: La Formula per l'Altezza di un Cilindro
Immaginate di dover progettare un contenitore cilindrico per un nuovo profumo, o di dover calcolare la quantità di acqua in una cisterna cilindrica. Questi sono solo due esempi di situazioni reali in cui la conoscenza della formula per l'altezza di un cilindro si rivela fondamentale.
Spesso, nella vita quotidiana, ci troviamo a confrontarci con forme geometriche senza nemmeno rendercene conto. Il cilindro, con la sua eleganza semplice, è una di queste. Ma come possiamo determinarne l'altezza conoscendo altri parametri come il volume e il raggio?
La risposta è più semplice di quanto si possa pensare: esiste una formula specifica che ci permette di farlo con facilità. Questa formula, alla portata di tutti, ci apre le porte a una comprensione più profonda del mondo che ci circonda.
In questo articolo, esploreremo a fondo il mondo della "formula altezza di un cilindro", svelandone i segreti, le applicazioni pratiche e le curiosità. Vi accompagneremo passo dopo passo alla scoperta di questo strumento matematico, fornendovi gli strumenti necessari per padroneggiarlo con sicurezza.
Che siate studenti alle prese con la geometria, appassionati di fai-da-te o semplicemente curiosi di espandere le vostre conoscenze, questo articolo vi fornirà una panoramica completa e dettagliata sulla "formula altezza di un cilindro".
Vantaggi e Svantaggi della Formula Altezza di un Cilindro
Come ogni strumento, anche la formula per l'altezza di un cilindro presenta vantaggi e svantaggi. Vediamoli nel dettaglio:
| Vantaggi | Svantaggi |
|---|---|
| Semplicità di utilizzo | Applicabilità limitata ai cilindri perfetti |
| Risparmio di tempo nei calcoli | Necessità di conoscere altri parametri del cilindro (volume, raggio) |
| Applicabilità in diversi ambiti |
Domande Frequenti sulla Formula Altezza di un Cilindro
1. Qual è la formula esatta per calcolare l'altezza di un cilindro?
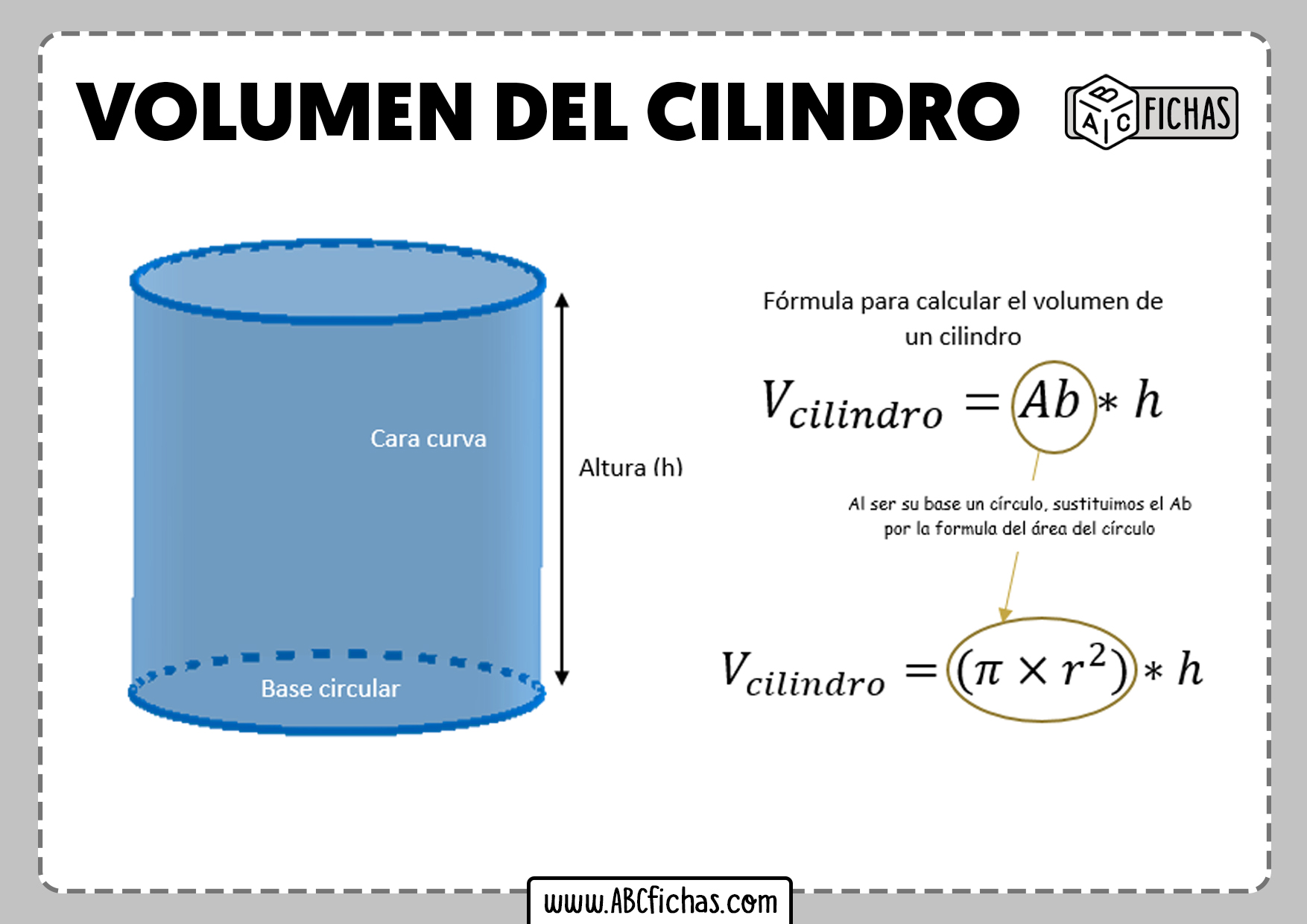
La formula è la seguente: h = V / (πr²), dove:
- h rappresenta l'altezza del cilindro
- V rappresenta il volume del cilindro
- π (pi greco) è una costante matematica che equivale a circa 3,14
- r rappresenta il raggio della base del cilindro
2. Cosa succede se non conosco il volume del cilindro?
Se non si conosce il volume, è possibile calcolarlo utilizzando altre formule, ad esempio conoscendo l'area della base e l'altezza (V = Ab * h).
3. Posso utilizzare questa formula per qualsiasi tipo di cilindro?
Sì, la formula è valida per qualsiasi cilindro perfetto, indipendentemente dalle sue dimensioni.
4. Ci sono altre formule per calcolare l'altezza di un cilindro?
Sì, esistono altre formule che utilizzano diversi parametri del cilindro, come la superficie laterale o la diagonale.
5. Quali sono le applicazioni pratiche di questa formula?
La formula è utile in diversi ambiti come l'ingegneria, l'architettura, il design e la fisica.
6. Quali sono gli errori più comuni nell'utilizzo di questa formula?
Gli errori più comuni riguardano l'utilizzo di unità di misura non coerenti e la confusione tra raggio e diametro.
7. Dove posso trovare ulteriori risorse sulla formula altezza di un cilindro?
Online sono disponibili numerose risorse, tra cui siti web specializzati in matematica e geometria.
8. Qual è l'importanza di comprendere la geometria dei solidi come il cilindro?
La geometria dei solidi è fondamentale per la comprensione del mondo che ci circonda e per la risoluzione di problemi pratici in diversi ambiti.
Conclusione
La formula per l'altezza di un cilindro, seppur apparentemente semplice, racchiude in sé un mondo di applicazioni pratiche e di connessioni con la realtà che ci circonda. Padroneggiare questa formula significa avere a disposizione uno strumento versatile e potente, applicabile in ambiti differenti. Che siate studenti, professionisti o semplicemente curiosi, la comprensione della geometria dei solidi, e in particolare del cilindro, vi permetterà di guardare al mondo con occhi diversi, cogliendo le connessioni tra forme, misure e volumi. Vi invitiamo a mettere in pratica quanto appreso, sperimentando e scoprendo le infinite sfaccettature di questa formula e del mondo della geometria.
Lettura seconda elementare italiano consigli per migliorarla
Trova i partner ideali la guida completa allelenco ufficiale di imprenditori fornitori
Fauteuil de jardin en rotin leclerc guida allacquisto e consigli
