Menyingkap Rahsia Bangun Ruang Sisi Datar: Dari Konsep ke Aplikasi
Pernahkah anda perhatikan bentuk-bentuk yang wujud di sekeliling kita? Kotak kasut yang tersusun rapi, piramid megah di Mesir, malah buku yang sedang anda baca, semuanya merupakan manifestasi fizikal konsep geometri yang dikenali sebagai bangun ruang sisi datar. Konsep asas ini menjadi asas kepada pemahaman kita tentang ruang dan bentuk, dan memainkan peranan penting dalam pelbagai bidang, dari seni bina hinggalah kejuruteraan.
Jauh sebelum manusia mencipta roda, tamadun purba telah pun mengaplikasikan prinsip-prinsip bangun ruang sisi datar dalam pembinaan monumen-monumen mengagumkan. Piramid Mesir, contohnya, merupakan bukti kehebatan penguasaan geometri oleh manusia zaman dahulu. Ketepatan dan ketelitian pembinaan struktur-struktur ini menunjukkan betapa pentingnya pemahaman tentang bangun ruang sisi datar dalam konteks sejarah.
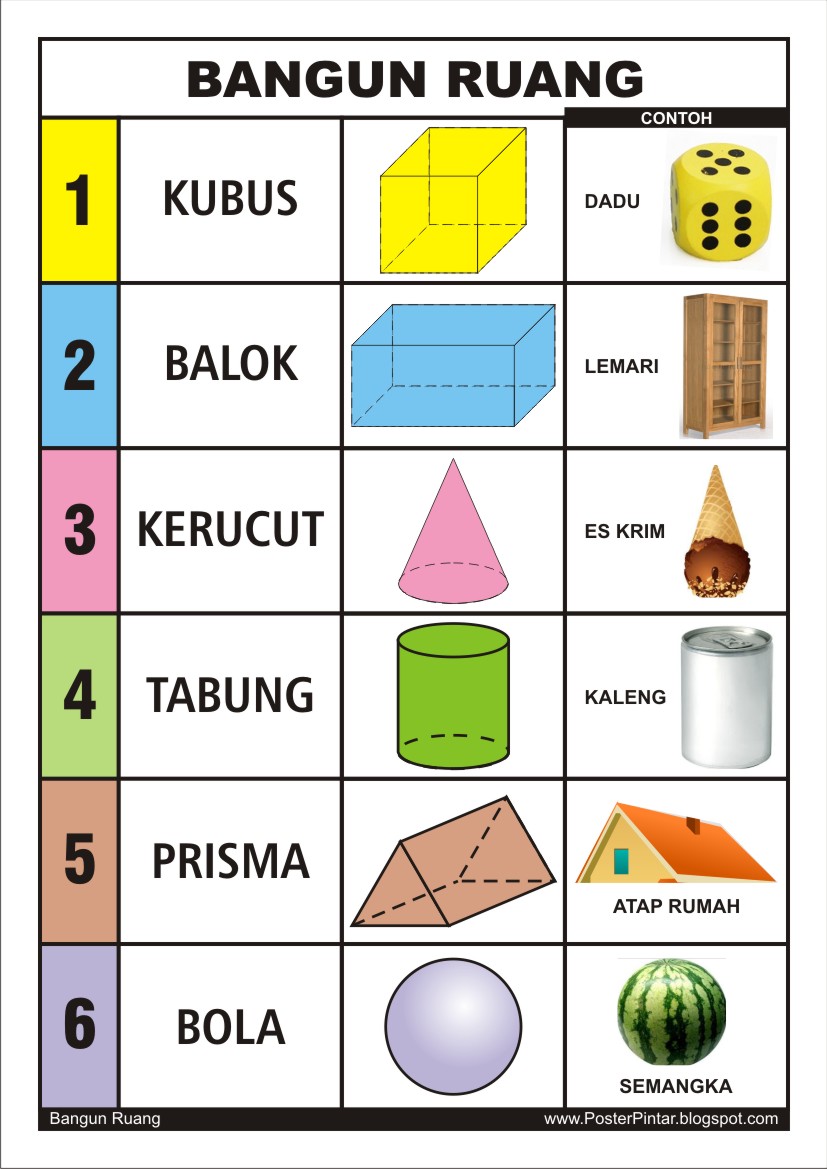
Secara ringkasnya, bangun ruang sisi datar merujuk kepada objek tiga dimensi yang dibatasi oleh permukaan rata. Permukaan rata ini, yang dikenali sebagai sisi, bersilang membentuk garis lurus yang dipanggil rusuk. Titik pertemuan antara rusuk-rusuk ini pula dikenali sebagai bucu. Kubus, piramid, prisma dan silinder merupakan contoh-contoh biasa bangun ruang sisi datar.
Kepentingan bangun ruang sisi datar melampaui batasan matematik. Dalam bidang seni bina, pemahaman tentang konsep ini membolehkan arkitek mereka bentuk bangunan yang kukuh dan estetik. Jurutera pula menggunakan prinsip bangun ruang sisi datar dalam mereka bentuk jambatan, terowong dan pelbagai lagi struktur penting. Malah, dalam kehidupan seharian, kita berinteraksi dengan objek-objek yang berbentuk bangun ruang sisi datar, seperti kotak, tin minuman dan perabot.
Salah satu manfaat utama mempelajari bangun ruang sisi datar ialah ia membantu kita memahami konsep ruang dan dimensi dengan lebih baik. Pengetahuan ini bukan sahaja penting dalam bidang STEM (Sains, Teknologi, Kejuruteraan dan Matematik), malah turut diaplikasikan dalam pelbagai bidang lain, seperti seni, reka bentuk dan juga sukan. Keupayaan untuk menggambarkan dan memanipulasi bentuk dalam ruang adalah kemahiran berharga yang boleh diaplikasikan dalam pelbagai konteks.
Kelebihan dan Kekurangan Mempelajari Bangun Ruang Sisi Datar
| Kelebihan | Kekurangan |
|---|---|
| Membantu memahami konsep ruang dan dimensi. | Boleh menjadi abstrak dan sukar difahami bagi sesetengah pelajar. |
| Dapat diaplikasikan dalam pelbagai bidang, seperti seni bina, kejuruteraan dan reka bentuk. | Memerlukan pemahaman tentang konsep geometri asas yang lain. |
Lima Amalan Terbaik dalam Mempelajari Bangun Ruang Sisi Datar
- Visualisasi: Gunakan bahan bantu belajar seperti model 3D atau lukisan untuk membantu menggambarkan bentuk dalam ruang.
- Praktikal: Bina model bangun ruang sisi datar menggunakan bahan-bahan seperti kertas, kadbod atau kayu.
- Aplikasi: Cari contoh-contoh bangun ruang sisi datar dalam persekitaran anda dan cuba kenal pasti ciri-cirinya.
- Latihan: Selesaikan pelbagai soalan latihan yang melibatkan pengiraan luas permukaan, isipadu dan ciri-ciri lain bangun ruang sisi datar.
- Kolaborasi: Bincangkan konsep dan penyelesaian masalah dengan rakan sekelas atau guru.
Lima Contoh Nyata Bangun Ruang Sisi Datar
- Kotak Kasut: Berbentuk kubus atau kuboid, digunakan untuk menyimpan kasut.
- Piramid: Struktur piramid di Mesir merupakan contoh piramid segi empat tepat, dibina sebagai makam firaun.
- Tin Minuman: Berbentuk silinder, digunakan untuk menyimpan minuman.
- Buku: Berbentuk kuboid, mengandungi maklumat dalam bentuk teks dan gambar.
- Meja: Permukaan meja biasanya berbentuk segi empat tepat atau bulatan, disokong oleh kaki meja yang berbentuk silinder atau kuboid.
Soalan Lazim tentang Bangun Ruang Sisi Datar
- Apakah perbezaan antara kubus dan kuboid? Kubus mempunyai enam sisi yang sama saiz dan bentuk (berbentuk segi empat sama), manakala kuboid mempunyai enam sisi yang terdiri daripada segi empat tepat.
- Apakah formula untuk mengira isipadu kubus? Isipadu kubus = sisi x sisi x sisi.
- Apakah ciri-ciri piramid? Piramid mempunyai tapak berbentuk poligon dan sisi-sisi berbentuk segi tiga yang bertemu di satu titik (apex).
Secara kesimpulannya, bangun ruang sisi datar merupakan konsep asas dalam geometri yang mempunyai aplikasi meluas dalam pelbagai bidang. Memahami ciri-ciri, jenis dan formula yang berkaitan dengan bangun ruang sisi datar bukan sahaja penting untuk kecemerlangan akademik, malah turut memupuk kemahiran berfikir kritis dan menyelesaikan masalah yang berguna dalam kehidupan seharian. Oleh itu, luangkanlah masa untuk meneroka dunia geometri yang menarik ini dan temui sendiri keajaibannya!
Semak status permohonan kwsp anda dengan id penjejakan
Sedekah vs zakat memahami perbezaan dan kepentingannya
Cara membuat sub bab 21 di word panduan lengkap dan mudah