Simbol Matematik: Menguasai Bahasa Nombor
Bayangkan cuba membaca novel tanpa mengetahui abjad, atau memahami muzik tanpa notasi. Itulah cabaran memahami matematik tanpa simbol-simbolnya. Simbol matematik adalah seperti huruf dalam abjad matematik, yang digabungkan untuk membentuk persamaan dan formula, yang membolehkan kita untuk menyatakan idea matematik yang kompleks dengan ringkas dan tepat. Tanpa simbol-simbol ini, dunia matematik akan menjadi lautan perkataan yang mengelirukan dan sukar difahami.
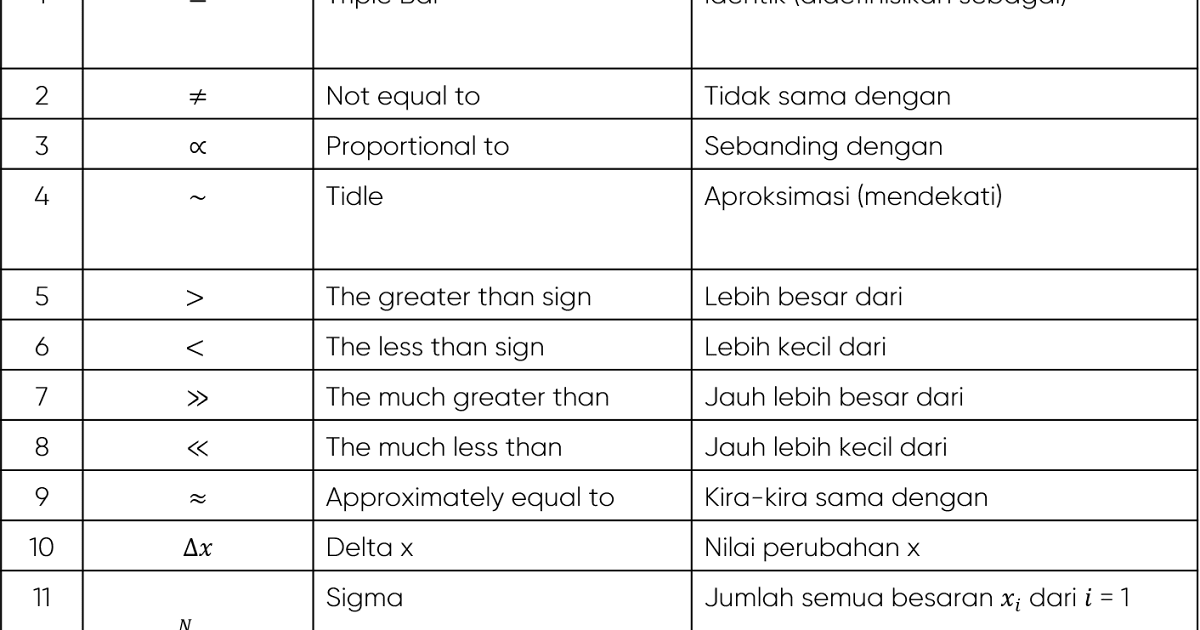
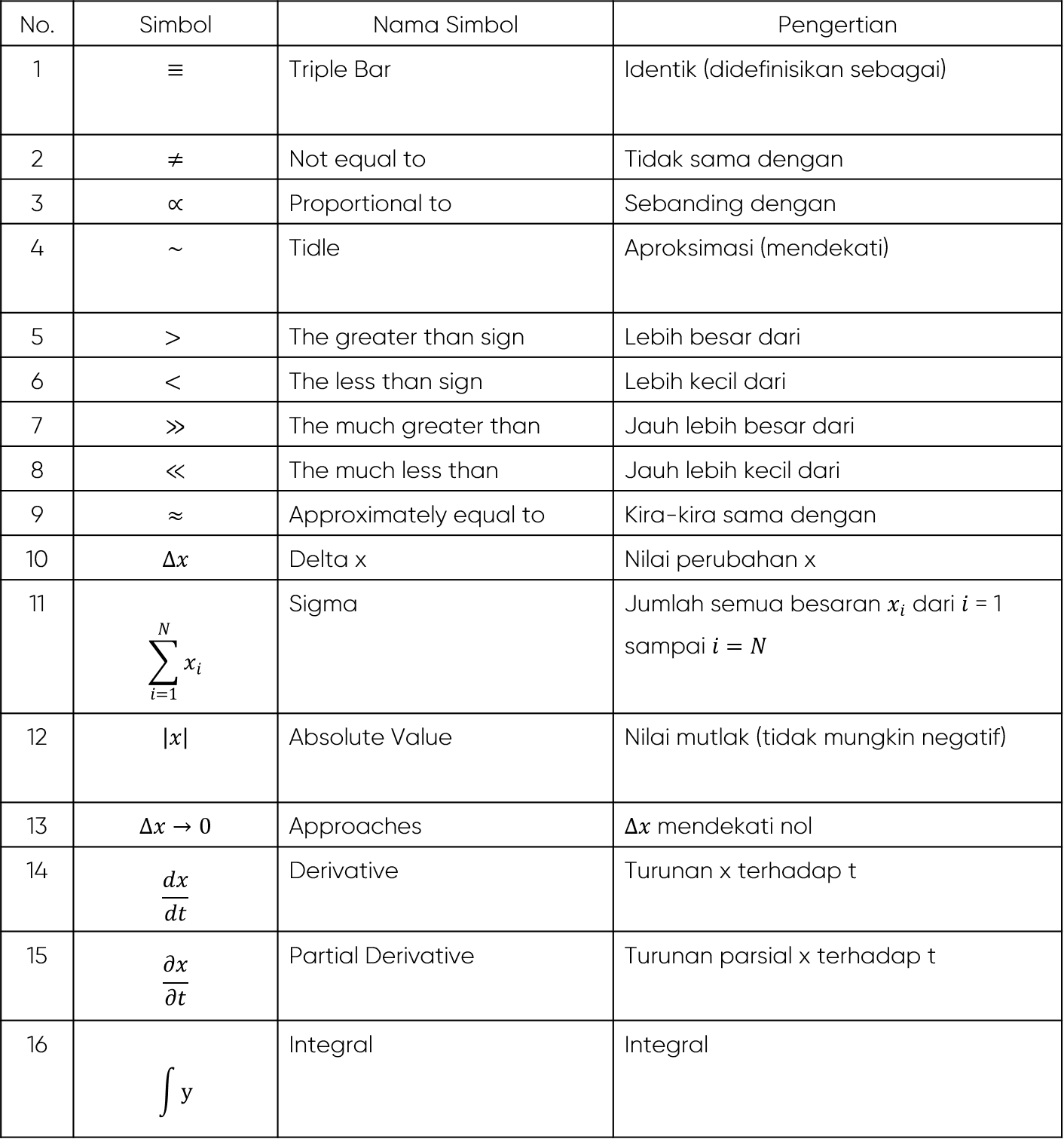
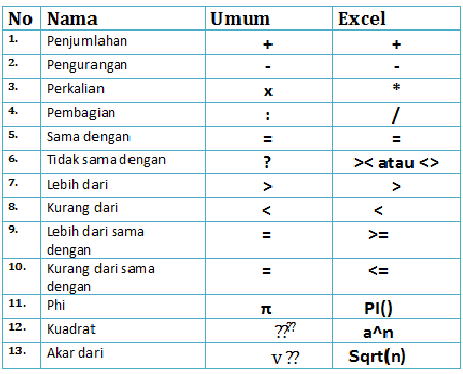
Daripada tanda tambah (+) dan tolak (-) yang asas kepada simbol integral dan derivatif yang lebih kompleks, setiap simbol memainkan peranan penting dalam menyampaikan konsep matematik dengan jelas dan ringkas. Keupayaan untuk membaca dan memahami simbol-simbol ini membuka kunci kepada pemahaman yang lebih mendalam tentang matematik dan aplikasinya dalam pelbagai bidang.
Sejarah simbol matematik berkait rapat dengan perkembangan matematik itu sendiri. Tamadun awal menggunakan sistem simbol yang mudah untuk mewakili nombor dan operasi asas. Contohnya, orang Mesir purba menggunakan hieroglif untuk mewakili nombor, manakala orang Babylon menggunakan sistem berasaskan 60.
Seiring dengan perkembangan matematik, begitu juga simbol-simbolnya. Ahli matematik Yunani purba seperti Euclid dan Pythagoras memperkenalkan simbol baharu dan membangunkan sistem notasi matematik yang lebih formal. Zaman Renaissance menyaksikan kemunculan simbol-simbol baharu seperti tanda sama (=) dan tanda darab (×), yang memudahkan lagi komunikasi idea matematik.
Penggunaan simbol dalam matematik adalah penting kerana beberapa sebab. Pertama, ia membolehkan kita untuk mewakili konsep matematik yang kompleks dengan cara yang ringkas dan ringkas. Bayangkan cuba menulis persamaan kuadratik dengan perkataan dan bukannya simbol - ia akan menjadi tugas yang sukar dan memakan masa! Kedua, simbol matematik adalah universal, bermakna ia difahami oleh ahli matematik di seluruh dunia, tanpa mengira bahasa mereka. Ketiga, simbol matematik membolehkan manipulasi dan penaakulan matematik yang tepat dan cekap.
Kelebihan dan Kekurangan Simbol Matematik
Walaupun terdapat banyak kelebihan menggunakan simbol matematik, terdapat juga beberapa kelemahan yang perlu dipertimbangkan:
| Kelebihan | Kekurangan |
|---|---|
| Komunikasi yang ringkas dan tepat | Boleh menjadi penghalang kepada pembelajaran bagi sesetengah orang |
| Bahasa matematik sejagat | Simbol yang berbeza boleh mempunyai makna yang berbeza dalam konteks yang berbeza |
| Memudahkan penaakulan dan manipulasi matematik | Penggunaan simbol yang berlebihan boleh menjadikan matematik kelihatan abstrak dan tidak dapat diakses |
Amalan Terbaik untuk Mempelajari Simbol Matematik
- Berlatih secara konsisten: Dedikasikan masa setiap hari untuk mengkaji dan mempraktikkan simbol matematik.
- Gunakan kad imbas: Tulis simbol pada satu sisi dan makna atau definisinya pada sisi yang lain.
- Selesaikan masalah latihan: Gunakan buku teks, laman web, atau aplikasi untuk menyelesaikan pelbagai masalah yang melibatkan simbol matematik yang berbeza.
- Cari corak dan hubungan: Daripada menghafal simbol secara membuta tuli, cuba cari corak dan hubungan antara simbol yang berbeza.
- Jangan takut untuk meminta bantuan: Jika anda menghadapi masalah dengan simbol tertentu, jangan teragak-agak untuk meminta bantuan daripada guru, tutor, atau rakan sekelas anda.
Soalan Lazim tentang Simbol Matematik
1. Apakah simbol infiniti?
Simbol infiniti (∞) mewakili konsep matematik sesuatu yang tidak terhingga atau tidak terbatas.
2. Apakah perbezaan antara tanda sama dengan (=) dan tanda kongruen (≅)?
Tanda sama dengan (=) menunjukkan bahawa dua kuantiti mempunyai nilai yang sama, manakala tanda kongruen (≅) menunjukkan bahawa dua bentuk geometri adalah sama dalam saiz dan bentuk.
3. Apakah simbol untuk punca kuasa dua?
Simbol untuk punca kuasa dua ialah √, juga dikenali sebagai tanda radikal.
4. Apakah simbol untuk pi (π)?
Simbol untuk pi (π) ialah huruf Yunani π, yang mewakili nisbah lilitan bulatan kepada diameternya.
5. Apakah simbol untuk fungsi?
Simbol untuk fungsi ialah f(x), di mana f ialah nama fungsi dan x ialah pemboleh ubah bebas.
6. Apakah simbol untuk pembezaan?
Simbol untuk pembezaan ialah d/dx, yang mewakili terbitan fungsi terhadap x.
7. Apakah simbol untuk pengamiran?
Simbol untuk pengamiran ialah ∫, yang mewakili pengamiran fungsi terhadap pemboleh ubah tertentu.
8. Apakah simbol untuk set kosong?
Simbol untuk set kosong ialah {}, atau Ø, yang mewakili set yang tidak mengandungi sebarang elemen.
Kesimpulan
Menguasai bahasa simbol matematik adalah penting untuk memahami dan menghargai keindahan dan kuasa matematik. Walaupun pada mulanya mungkin kelihatan menakutkan, ingatlah bahawa setiap simbol hanyalah alat yang direka untuk membantu kita memahami dan menyelesaikan masalah. Dengan dedikasi, latihan, dan rasa ingin tahu, sesiapa sahaja boleh mempelajari dan menghargai simbol-simbol yang membentuk asas matematik.
Menakluk soalan rbt tahun 5 akhir tahun rahsia kejayaan terbongkar
Whatsapp media sosial atau aplikasi pemesejan
Lukisan alat dan bahan kerja kursus psv