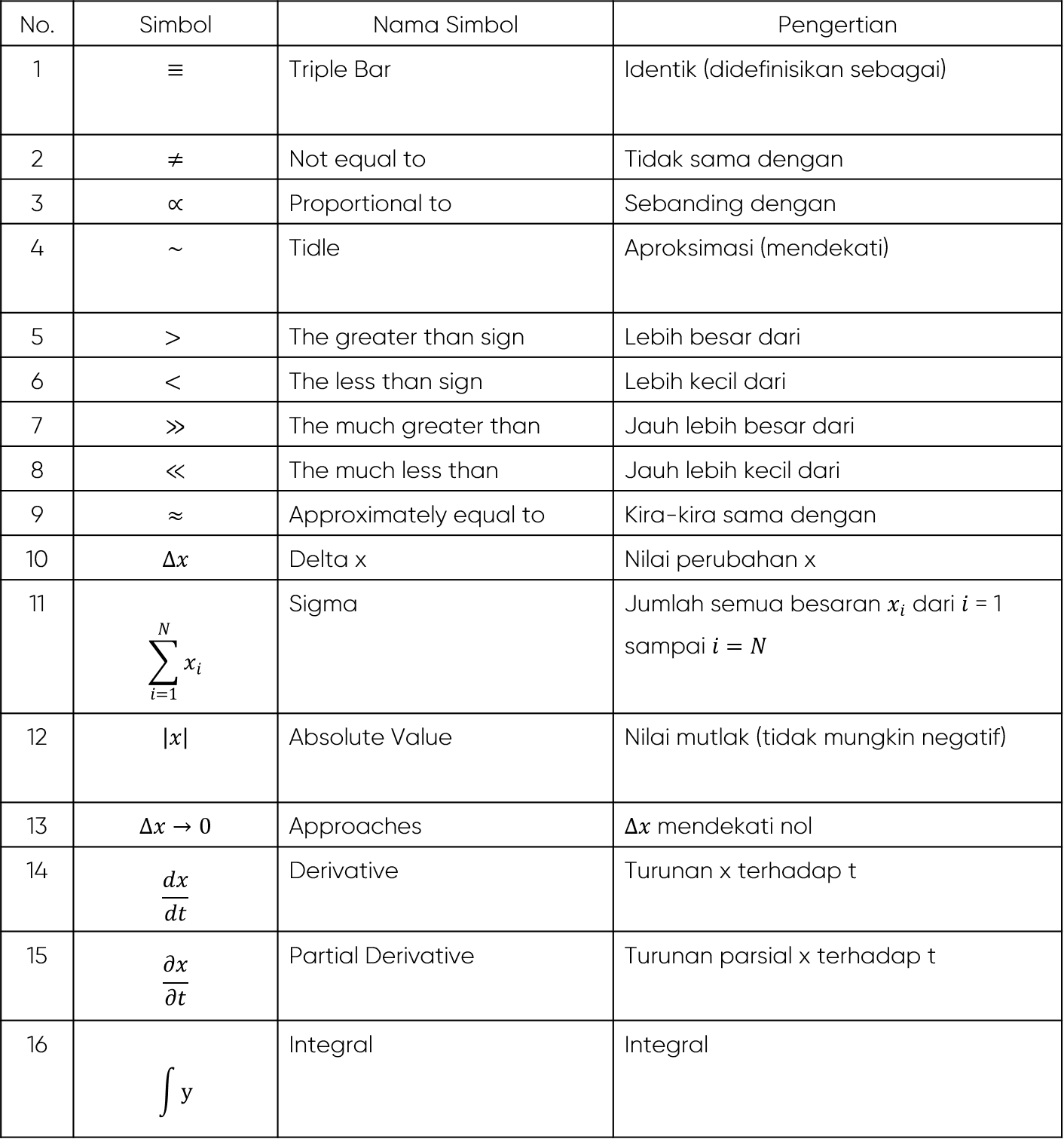
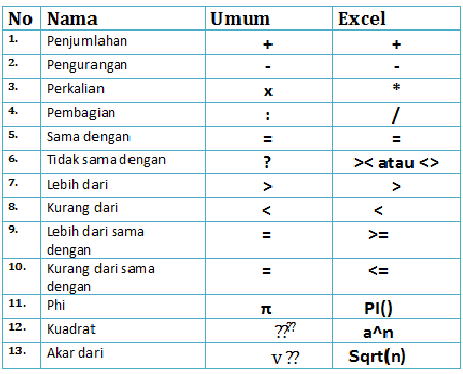
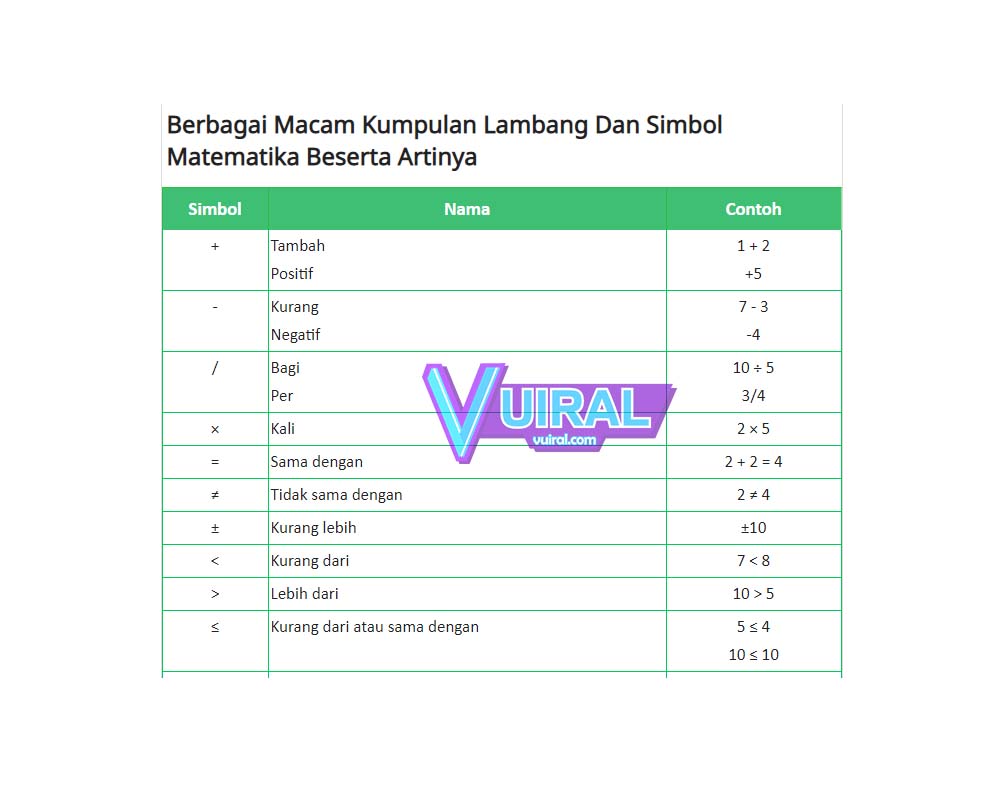
Simbol Misteri: Menyelami Rahsia Simbol '∈' dalam Matematik
Pernahkah anda terserempak dengan simbol aneh '∈' ketika melayari persamaan matematik? Jangan risau, anda tidak keseorangan! Simbol ini, yang kelihatan seperti huruf 'E' yang bergaya, memainkan peranan penting dalam dunia matematik. Ia dikenali sebagai 'simbol elemen' atau 'simbol kepunyaan'.
Bayangkan anda mempunyai sekumpulan buah-buahan dan anda ingin menunjukkan bahawa sebiji epal adalah sebahagian daripada kumpulan itu. Di sinilah simbol '∈' muncul. Jika 'A' mewakili kumpulan buah-buahan dan 'e' mewakili epal, pernyataan 'e ∈ A' bermaksud "epal adalah elemen dalam kumpulan A" atau "epal kepunyaan A".
Simbol '∈' diperkenalkan oleh ahli matematik Itali, Giuseppe Peano, pada akhir abad ke-19. Peano, yang terkenal dengan sumbangannya dalam logik matematik dan teori set, memilih simbol ini berdasarkan perkataan Greek 'εστί' yang bermaksud "adalah".
Simbol '∈' mungkin kelihatan kecil dan tidak penting, tetapi ia adalah asas kepada banyak konsep matematik, terutamanya dalam teori set. Ia membantu kita untuk mendefinisikan set, hubungan antara elemen dan set, dan untuk membina struktur matematik yang lebih kompleks.
Penggunaan simbol '∈' tidak terhad kepada matematik sahaja. Ia juga digunakan dalam bidang lain seperti sains komputer dan logik. Sebagai contoh, dalam pangkalan data, simbol '∈' boleh digunakan untuk menunjukkan bahawa rekod tertentu adalah sebahagian daripada jadual.
Mari kita lihat beberapa contoh bagaimana simbol '∈' digunakan dalam matematik:
- Jika B = {1, 2, 3, 4, 5} dan x = 3, maka x ∈ B kerana 3 adalah elemen dalam set B.
- Jika C = {huruf vokal} dan a = a, maka a ∈ C kerana 'a' adalah huruf vokal.
Simbol '∈' mempunyai pasangannya iaitu '∉' yang bermaksud "bukan elemen" atau "tidak kepunyaan". Contohnya, jika D = {haiwan berkaki dua} dan s = ular, maka s ∉ D kerana ular bukan haiwan berkaki dua.
Meskipun kelihatan mudah, simbol '∈' adalah alat yang sangat kuat dalam matematik. Ia membantu kita untuk menyatakan konsep kepunyaan dengan jelas dan ringkas, dan membentuk asas untuk pemahaman yang lebih mendalam tentang teori set dan konsep matematik yang lain.
Kelebihan dan Kekurangan Simbol '∈'
| Kelebihan | Kekurangan |
|---|---|
| Mudah difahami dan digunakan. | Boleh mengelirukan dengan simbol lain seperti '€' (Euro). |
| Membuat pernyataan matematik lebih ringkas. | - |
| Digunakan secara meluas dalam pelbagai bidang. | - |
5 Amalan Terbaik Menggunakan Simbol '∈'
- Pastikan anda memahami perbezaan antara simbol '∈' dan '∉'.
- Gunakan simbol '∈' dengan betul apabila menyatakan kepunyaan elemen dalam set.
- Pastikan set yang dirujuk ditakrifkan dengan jelas.
- Gunakan simbol '∈' bersama-sama dengan simbol matematik lain untuk membentuk pernyataan matematik yang kompleks.
- Berlatih menggunakan simbol '∈' dalam pelbagai konteks matematik untuk meningkatkan pemahaman anda.
5 Contoh Sebenar Simbol '∈' dalam Matematik
- Dalam teori kebarangkalian, simbol '∈' digunakan untuk menunjukkan bahawa suatu peristiwa adalah sebahagian daripada ruang sampel.
- Dalam algebra linear, simbol '∈' digunakan untuk menunjukkan bahawa suatu vektor adalah elemen dalam suatu ruang vektor.
- Dalam analisis nyata, simbol '∈' digunakan untuk menunjukkan bahawa suatu nombor adalah elemen dalam suatu selang.
- Dalam topologi, simbol '∈' digunakan untuk menunjukkan bahawa suatu titik adalah elemen dalam suatu set terbuka.
- Dalam teori graf, simbol '∈' digunakan untuk menunjukkan bahawa suatu bucu adalah elemen dalam suatu graf.
Soalan Lazim Berkenaan Simbol '∈'
1. Apakah perbezaan antara simbol '∈' dan '⊆'?
Simbol '∈' menunjukkan kepunyaan elemen dalam set, manakala '⊆' menunjukkan subset. Jika A ⊆ B, maka setiap elemen dalam A juga merupakan elemen dalam B.
2. Bolehkah simbol '∈' digunakan dengan set kosong?
Tidak, set kosong tidak mempunyai elemen, jadi tidak ada elemen yang boleh menjadi '∈' set kosong.
3. Apakah kepentingan simbol '∈' dalam matematik?
Simbol '∈' adalah asas kepada teori set dan membolehkan kita untuk mendefinisikan set, hubungan antara elemen dan set, dan untuk membina struktur matematik yang lebih kompleks.
Simbol '∈' mungkin kelihatan kecil dan tidak penting pada pandangan pertama, tetapi ia adalah salah satu simbol yang paling asas dan penting dalam matematik. Memahami simbol ini membuka jalan untuk pemahaman yang lebih mendalam tentang teori set dan pelbagai cabang matematik yang lain. Teruskan belajar dan meneroka dunia matematik yang menarik ini!
Kajian tokoh tentang media sosial
Mudahnya berpindah panduan lengkap contoh surat permohonan pindah alamat rumah
Surat permohonan keringanan bayaran jimat duit dengan cara yang betul
