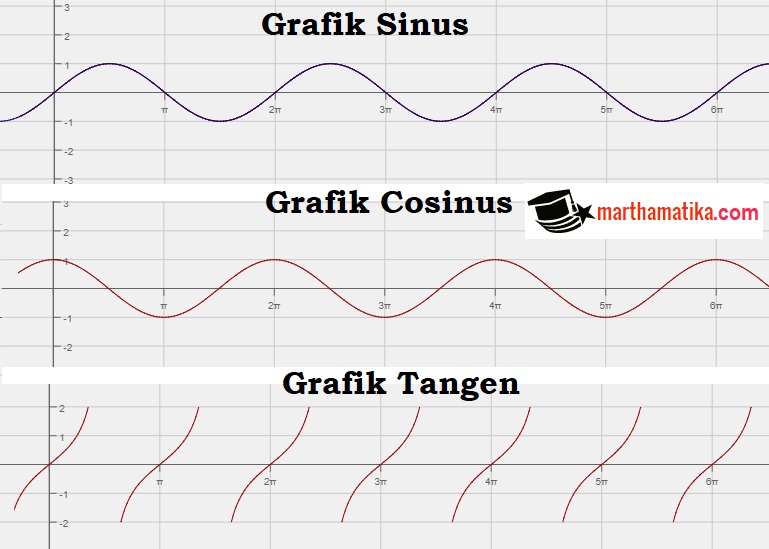
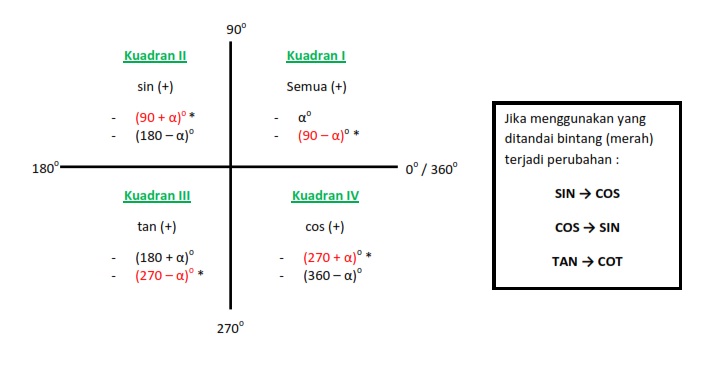
Het verschil tussen sinus en cosinus: een complete gids
Wiskunde. Voor veel mensen roept het woord beelden op van saaie lessen en eindeloze formules. Maar wist je dat wiskunde ook ontzettend interessant en relevant kan zijn? Neem nou sinus en cosinus, twee trigonometrische functies die onmisbaar zijn in tal van vakgebieden, van architectuur tot muziek! In deze blog duiken we in de wereld van sinus en cosinus, en ontdekken we wat ze precies inhouden en waarom ze zo belangrijk zijn.
Sinus en cosinus, vaak afgekort tot 'sin' en 'cos', draaien om de relaties tussen hoeken en zijden in rechthoekige driehoeken. Ze vertellen ons hoe de lengte van een zijde zich verhoudt tot de hoekgrootte. Stel je voor: je staat op de grond en kijkt naar een hoge toren. De hoek tussen de grond en je blik naar de top van de toren noemen we de 'elevatiehoek'. Met behulp van sinus en cosinus kunnen we dan de hoogte van de toren berekenen, zelfs zonder een meetlint!
De oorsprong van sinus en cosinus gaat terug tot de oude Griekse beschaving, waar wiskundigen als Hipparchus en Ptolemaeus de basis legden voor de trigonometrie. Door de eeuwen heen zijn deze functies verder ontwikkeld en verfijnd, en tegenwoordig spelen ze een cruciale rol in uiteenlopende disciplines.
Maar wat is nu precies het verschil tussen sinus en cosinus? Simpel gezegd: sinus kijkt naar de verhouding tussen de overstaande zijde en de schuine zijde van een rechthoekige driehoek, terwijl cosinus de verhouding tussen de aanliggende zijde en de schuine zijde beschrijft. Denk terug aan het voorbeeld van de toren. De sinus van de elevatiehoek geeft de verhouding tussen de hoogte van de toren (overstaande zijde) en de afstand van jou tot de top (schuine zijde). De cosinus van diezelfde hoek beschrijft dan weer de verhouding tussen de afstand van jou tot de voet van de toren (aanliggende zijde) en de afstand van jou tot de top (schuine zijde).
De toepassingen van sinus en cosinus zijn eindeloos! In de natuurkunde worden ze gebruikt om golfbewegingen te beschrijven, zoals licht en geluid. Architecten gebruiken ze om de stabiliteit van gebouwen te berekenen. En in de muziek? Daar bepalen sinus en cosinus de toonhoogte en klankkleur van muzieknoten!
Voordelen van Sinus en Cosinus
Het begrijpen van sinus en cosinus biedt tal van voordelen, zoals:
- Problemen met driehoeken oplossen: Sinus en cosinus stellen ons in staat om ontbrekende zijden en hoeken in rechthoekige driehoeken te berekenen. Dit is met name handig in vakgebieden als bouwkunde en navigatie.
- Periodieke verschijnselen beschrijven: Veel fenomenen in de natuur, zoals getijden, seizoenen en geluidsgolven, vertonen een periodiek patroon. Sinus en cosinus zijn ideaal om deze patronen te modelleren en te analyseren.
- Complexe berekeningen vereenvoudigen: In de wiskunde en natuurkunde worden sinus en cosinus vaak gebruikt om complexe problemen te vereenvoudigen en op te lossen. Ze vormen de basis voor geavanceerde wiskundige concepten zoals Fourieranalyse en complexe getallen.
Veelgestelde vragen over Sinus en Cosinus
Hier zijn enkele veelgestelde vragen over sinus en cosinus:
- Wat is het verschil tussen sinus, cosinus en tangens?
- Hoe bereken ik de sinus en cosinus van een hoek zonder rekenmachine?
- Wat zijn de toepassingen van sinus en cosinus in de praktijk?
- Hoe kan ik sinus en cosinus gebruiken om de hoogte van een gebouw te meten?
- Wat zijn de belangrijkste formules met sinus en cosinus?
- Hoe kan ik sinus en cosinus visualiseren met behulp van de eenheidscirkel?
- Waar kan ik meer informatie vinden over sinus en cosinus?
- Zijn er online tools of apps die mij kunnen helpen met sinus en cosinus berekeningen?
Conclusie
Sinus en cosinus mogen dan misschien abstract lijken op het eerste gezicht, ze zijn onmisbaar in ons dagelijks leven en spelen een cruciale rol in tal van vakgebieden. Van het berekenen van de hoogte van een gebouw tot het beschrijven van de beweging van geluidsgolven, sinus en cosinus stellen ons in staat om de wereld om ons heen beter te begrijpen. Dus de volgende keer dat je wiskunde een beetje saai vindt, denk dan aan sinus en cosinus, en al hun fascinerende toepassingen!
Heel holland bakt gemist zo kijk je afleveringen terug
Wie regeert de turnwereld de beste turnsters van dit moment
Marc van den bossche een verkenning van zijn filosofische inzichten
