Hoogte Driehoek Berekenen Ontdek de Methoden
De hoogte van een driehoek bepalen: een essentiële vaardigheid in de meetkunde. Of je nu een student bent, een professional in een technisch veld, of gewoon je wiskundige kennis wilt opfrissen, het begrijpen van hoe je de hoogte van een driehoek berekent is fundamenteel.
Maar hoe pak je dit aan? Er zijn verschillende methoden om de hoogte van een driehoek te vinden, afhankelijk van de beschikbare informatie. Van het gebruik van de basis en de oppervlakte tot het toepassen van de stelling van Pythagoras in rechthoekige driehoeken, de mogelijkheden zijn divers.
Het berekenen van de hoogte van een driehoek is meer dan alleen een wiskundige oefening. Het heeft praktische toepassingen in diverse gebieden, zoals architectuur, engineering en landmeting. Stel je voor dat je de oppervlakte van een driehoekig perceel grond moet berekenen, of de hoogte van een dak moet bepalen voor een bouwproject. In dergelijke situaties is het kennen van de juiste methode om de hoogte van een driehoek te berekenen cruciaal.
De oorsprong van deze berekeningen gaat terug tot de oude Grieken, met name tot wiskundigen zoals Euclides en Pythagoras. Zij legden de basis voor de meetkunde zoals we die vandaag de dag kennen, inclusief de principes die we gebruiken om de hoogte van een driehoek te bepalen.
Een veelvoorkomend probleem bij het berekenen van de hoogte is het ontbreken van de juiste gegevens. Soms is alleen de lengte van de zijden bekend, en andere keren is alleen de oppervlakte en de basis gegeven. Het is belangrijk om de juiste formule te kiezen op basis van de beschikbare informatie.
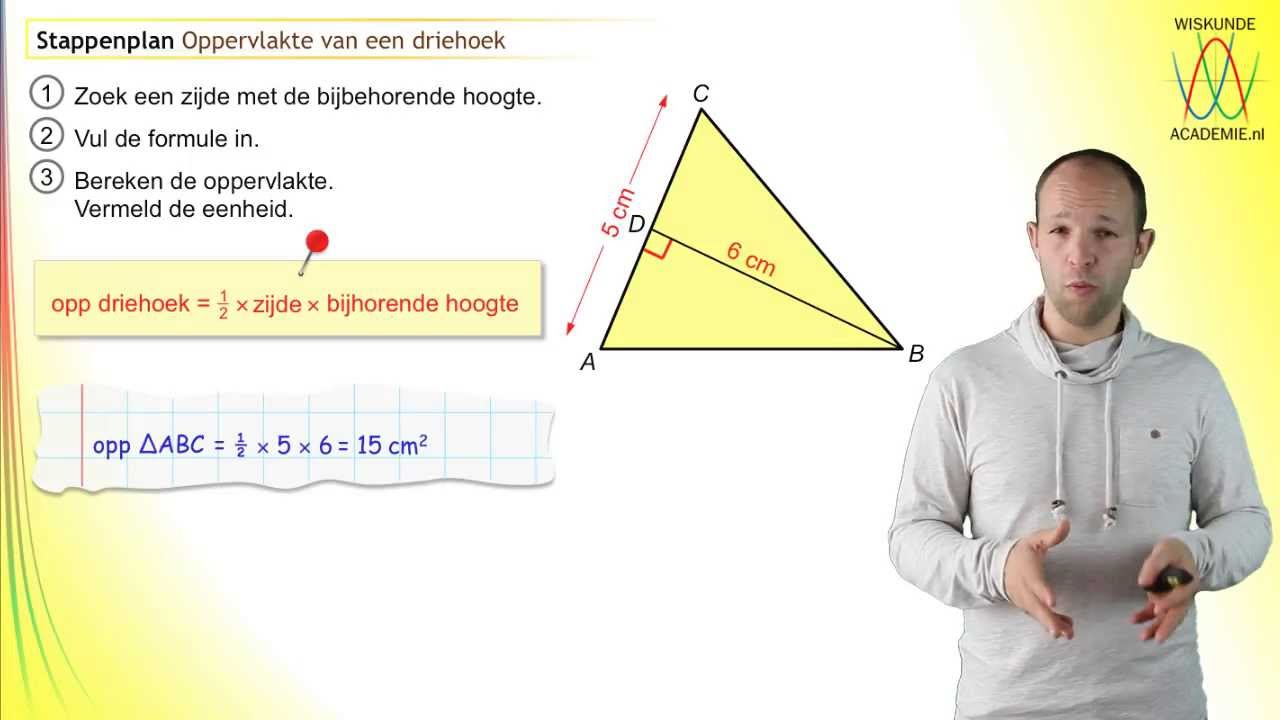
De hoogte van een driehoek is de loodrechte afstand van een hoekpunt naar de tegenoverliggende zijde (de basis). Een driehoek heeft drie hoogtes, één voor elke basis. Om de hoogte te berekenen met de oppervlakte en de basis, gebruik je de formule: hoogte = (2 * oppervlakte) / basis. Bijvoorbeeld, als de oppervlakte 20 cm² is en de basis 5 cm, dan is de hoogte (2 * 20) / 5 = 8 cm.
Voordelen van het kunnen berekenen van de hoogte van een driehoek zijn: 1. Oppervlakteberekening: Essentieel voor landmeting en constructie. 2. Volumeberekening van prisma's en piramides: De hoogte van de driehoekige basis is nodig. 3. Problemen oplossen in de natuurkunde en engineering: Veel fysische problemen vereisen kennis van driehoeksmeetkunde.
Een actieplan om de hoogte te berekenen: 1. Identificeer de bekende gegevens. 2. Kies de juiste formule. 3. Voer de waarden in en bereken de hoogte.
Checklist: 1. Heb ik de basis en de oppervlakte? 2. Heb ik de lengte van de zijden? 3. Is de driehoek rechthoekig?
Stap-voor-stap handleiding: 1. Bepaal welke gegevens bekend zijn. 2. Kies de juiste formule (oppervlakte en basis, Pythagoras, etc.). 3. Substitueer de waarden in de formule. 4. Bereken de hoogte.
Aanbevolen websites: wiskunde.net, geogebra.org
Voor- en nadelen van hoogteberekening
| Voordelen | Nadelen |
|---|---|
| Essentieel voor oppervlakteberekening | Kan complex zijn bij onvolledige gegevens |
Beste praktijken: 1. Gebruik de juiste eenheden. 2. Controleer je antwoord. 3. Teken een schets. 4. Gebruik een rekenmachine. 5. Leer de verschillende formules.
Concrete voorbeelden: 1. Basis=5, oppervlakte=10, hoogte=4. 2. Basis=8, oppervlakte=24, hoogte=6. 3. Basis=10, oppervlakte=30, hoogte=6. 4. Basis=4, oppervlakte=8, hoogte=4. 5. Basis=6, oppervlakte=18, hoogte=6.
Uitdagingen en oplossingen: 1. Onbekende basis: Gebruik andere gegevens en formules. 2. Complexe driehoeken: Verdeel in kleinere driehoeken. 3. Onnauwkeurige metingen: Gebruik nauwkeurige meetinstrumenten. 4. Verkeerde formule: Controleer de formule en de gegevens. 5. Rekenfouten: Gebruik een rekenmachine en controleer je berekeningen.
FAQ: 1. Wat is de hoogte van een driehoek? De loodrechte afstand van een hoekpunt tot de tegenoverliggende zijde. 2. Hoe bereken ik de hoogte met de oppervlakte en basis? hoogte = (2 * oppervlakte) / basis. 3. Wat als ik alleen de zijden ken? Gebruik de formule van Heron of trigonometrie. 4. Hoeveel hoogtes heeft een driehoek? Drie. 5. Wat is de stelling van Pythagoras? a² + b² = c² (voor rechthoekige driehoeken). 6. Kan ik online tools gebruiken om de hoogte te berekenen? Ja, er zijn diverse online rekenmachines en websites beschikbaar. 7. Wat is het belang van het berekenen van de hoogte? Essentieel voor oppervlakte- en volumeberekeningen, en diverse toepassingen in wetenschap en techniek. 8. Waar kan ik meer informatie vinden over driehoeksmeetkunde? In wiskundeboeken, online bronnen en educatieve websites.
Tips en trucs: Teken altijd een schets van de driehoek. Label de zijden en hoeken. Gebruik een rekenmachine voor nauwkeurige berekeningen. Oefen met verschillende voorbeelden.
Kortom, het berekenen van de hoogte van een driehoek is een essentiële vaardigheid met brede toepassingen. Of je nu een student bent die worstelt met meetkunde, een professional die nauwkeurige berekeningen nodig heeft, of gewoon je wiskundige kennis wilt opfrissen, het beheersen van deze vaardigheid is waardevol. Door de verschillende methoden, formules en praktische tips te begrijpen, kun je met vertrouwen de hoogte van elke driehoek berekenen. Blijf oefenen met diverse voorbeelden en raadpleeg online bronnen en leerboeken voor verdere verdieping in de fascinerende wereld van de driehoeksmeetkunde. Het begrijpen van dit concept opent deuren naar een beter begrip van wiskunde en haar toepassingen in de wereld om ons heen. Neem de tijd om te oefenen en ontdek de vele manieren waarop deze kennis je kan helpen in je academische en professionele leven.
Ontdek de mogelijkheden van albert road south melbourne 132 136
Willem hussem te koop ontdek de betoverende wereld van zijn kunst
De betekenis van titel von green day saviors ontrafeld