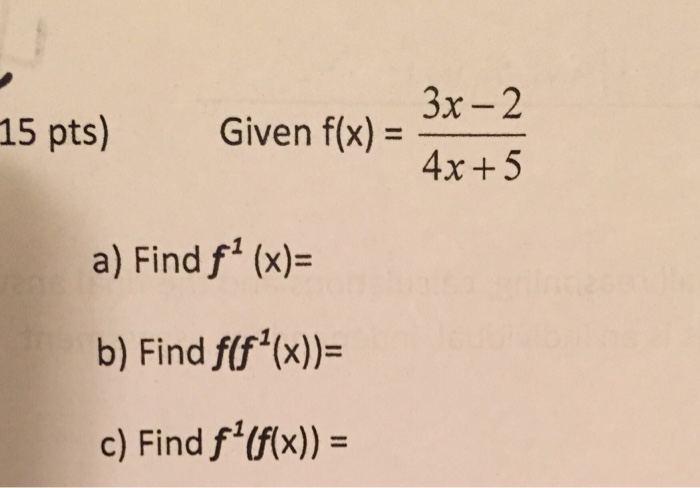Inverse Functie vinden: f(x) = (3x+2)/x
Hoe vind je de inverse van een functie? Stel je voor dat je een functie hebt die een input neemt en een output produceert. De inverse functie doet precies het tegenovergestelde: hij neemt de output van de originele functie en geeft de oorspronkelijke input terug. Dit concept is essentieel in de wiskunde en heeft vele toepassingen, bijvoorbeeld in de cryptografie en signaalverwerking.
In dit artikel duiken we in de wereld van inverse functies en richten we ons specifiek op het vinden van de inverse van f(x) = (3x+2)/x. We zullen de stappen doorlopen, voorbeelden bekijken en veelgestelde vragen beantwoorden om je te helpen dit concept volledig te begrijpen.
Het vinden van de inverse van een functie is als het terugdraaien van een proces. Als we bijvoorbeeld f(x) = 2x hebben, verdubbelt de functie de input. De inverse functie, f-1(x) = x/2, deelt de input door twee, waardoor we terugkeren naar de oorspronkelijke waarde.
De functie f(x) = (3x+2)/x is iets complexer. Om de inverse te vinden, moeten we x en y verwisselen en vervolgens de vergelijking herschrijven om y uit te drukken in termen van x. Dit proces kan soms lastig zijn, maar met oefening wordt het makkelijker.
Het begrijpen van inverse functies is niet alleen belangrijk voor wiskundige problemen, maar ook voor het oplossen van problemen in de echte wereld. Denk bijvoorbeeld aan het omrekenen van temperaturen tussen Celsius en Fahrenheit. De formules voor deze conversies zijn inverse functies van elkaar.
Om de inverse van f(x) = (3x+2)/x te vinden, verwisselen we x en y: x = (3y+2)/y. Vervolgens lossen we op voor y: xy = 3y + 2, xy - 3y = 2, y(x - 3) = 2, en uiteindelijk, y = 2/(x-3). Dus, f-1(x) = 2/(x-3).
Een veelgestelde vraag is: bestaat de inverse functie altijd? Het antwoord is nee. Een functie heeft alleen een inverse als hij bijectief is, wat betekent dat elke output overeenkomt met precies één input en vice versa. Dit kan worden gecontroleerd met de horizontale lijntest.
Voorbeeld: Als f(1) = (3(1)+2)/1 = 5, dan moet f-1(5) = 2/(5-3) = 1. Dit bevestigt onze berekening van de inverse functie.
Voordelen van het begrijpen van inverse functies:
1. Oplossen van vergelijkingen: Inverse functies kunnen worden gebruikt om complexe vergelijkingen op te lossen.
2. Modelleren van real-world situaties: Veel relaties in de echte wereld kunnen worden gemodelleerd met behulp van inverse functies.
3. Begrip van functiegedrag: Het analyseren van de inverse functie kan inzicht geven in het gedrag van de originele functie.
FAQ:
1. Wat is een inverse functie? Een functie die het effect van de originele functie omkeert.
2. Hoe vind je de inverse van een functie? Verwissel x en y en los op voor y.
3. Bestaat de inverse functie altijd? Nee, alleen voor bijectieve functies.
4. Wat is de horizontale lijntest? Een test om te bepalen of een functie een inverse heeft.
5. Wat is het domein van de inverse functie? Het bereik van de originele functie.
6. Wat is het bereik van de inverse functie? Het domein van de originele functie.
7. Hoe controleer je of je de inverse correct hebt berekend? Door de samenstelling van de functie en zijn inverse te berekenen.
8. Waar kan ik meer informatie vinden over inverse functies? Zoek online naar "inverse functions" of raadpleeg een wiskundeboek.
Conclusie
Het vinden van de inverse van een functie, zoals f(x) = (3x+2)/x, is een belangrijke vaardigheid in de wiskunde. Door de stappen te begrijpen en te oefenen met voorbeelden, kun je dit concept beheersen. Inverse functies hebben vele toepassingen, van het oplossen van vergelijkingen tot het modelleren van real-world situaties. Het is essentieel om de eigenschappen van inverse functies te begrijpen, zoals het domein en bereik, en om te controleren of de berekende inverse correct is. Blijf oefenen en ontdek de fascinerende wereld van inverse functies! Dit begrip opent de deur naar een dieper begrip van functies en hun gedrag, en biedt krachtige tools voor het oplossen van wiskundige en praktische problemen. Door de relatie tussen een functie en zijn inverse te begrijpen, kunnen we complexe systemen beter analyseren en manipuleren. Ga verder met het verkennen van dit concept en ontdek de vele mogelijkheden die het biedt.
Ontdek de magie van titel generators voor boeken
Ontdek je nieuwe look met een baard
De geboorte van de fiets ontdek het jaar van uitvinding