Ontdek de geheimen van driehoekszijden: Bereken ze als een pro!
Driehoeken, die ogenschijnlijk simpele geometrische vormen, herbergen een wereld aan wiskundige geheimen. Een van de meest fundamentele vragen die we ons kunnen stellen is: hoe berekenen we de lengte van hun zijden? Deze vraag, hoe simpel ze ook lijkt, opent de deur naar een fascinerende wereld van wiskundige principes en praktische toepassingen.
De lengte van een driehoekszijde bepalen is essentieel in talloze disciplines, van architectuur en engineering tot landmeetkunde en zelfs computergraphics. Stel je voor dat je een brug ontwerpt, een gebouw bouwt of een navigatiesysteem programmeert - zonder de mogelijkheid om driehoekszijden te berekenen, zouden deze taken onmogelijk zijn.
Er zijn verschillende manieren om de zijde van een driehoek te berekenen, afhankelijk van de beschikbare informatie. Heb je twee zijden en de ingesloten hoek? Dan biedt de cosinusregel uitkomst. Ken je twee hoeken en een zijde? Dan is de sinusregel je beste vriend. En natuurlijk, voor rechthoekige driehoeken is de Stelling van Pythagoras een onmisbaar hulpmiddel.
Het beheersen van deze technieken stelt je niet alleen in staat om complexe geometrische problemen op te lossen, maar het traint ook je analytische denkvermogen en probleemoplossende vaardigheden. Het begrijpen van de onderliggende principes van driehoeksmeetkunde opent de deur naar een dieper begrip van de wereld om ons heen.
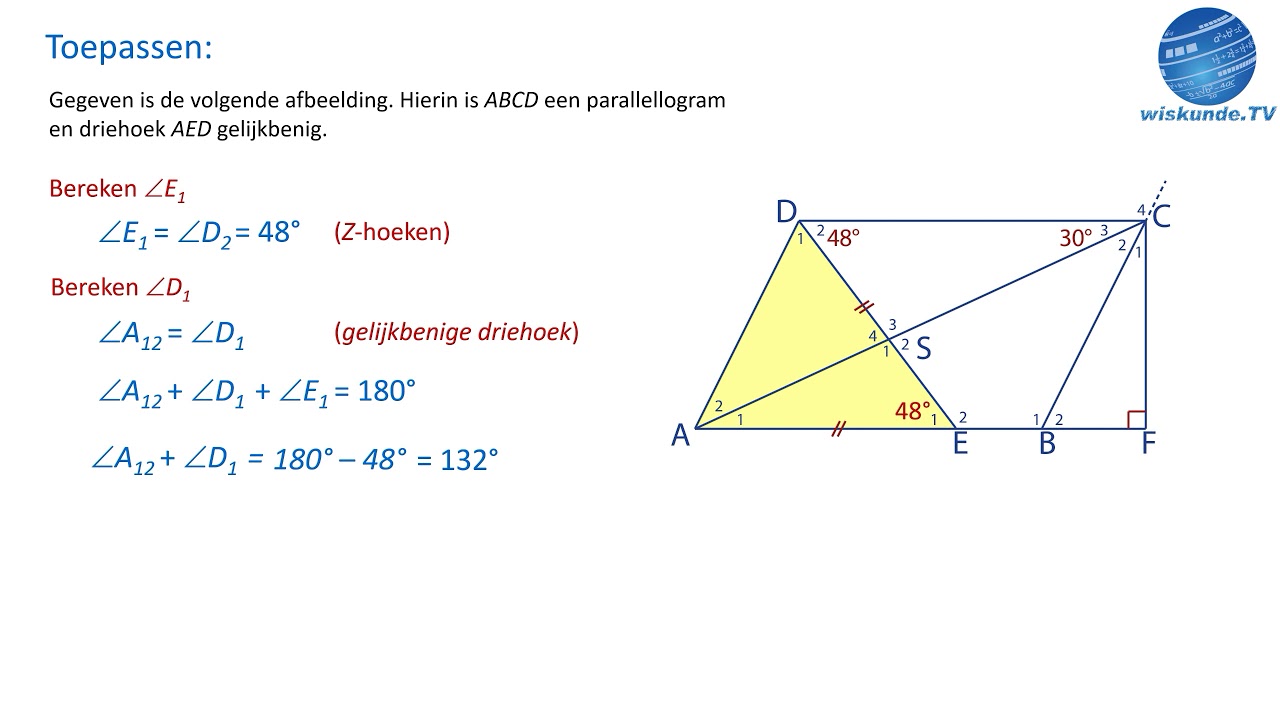
Laten we ons nu verdiepen in de verschillende methoden om de lengte van een driehoekszijde te berekenen, en ontdekken hoe deze technieken in de praktijk kunnen worden toegepast.
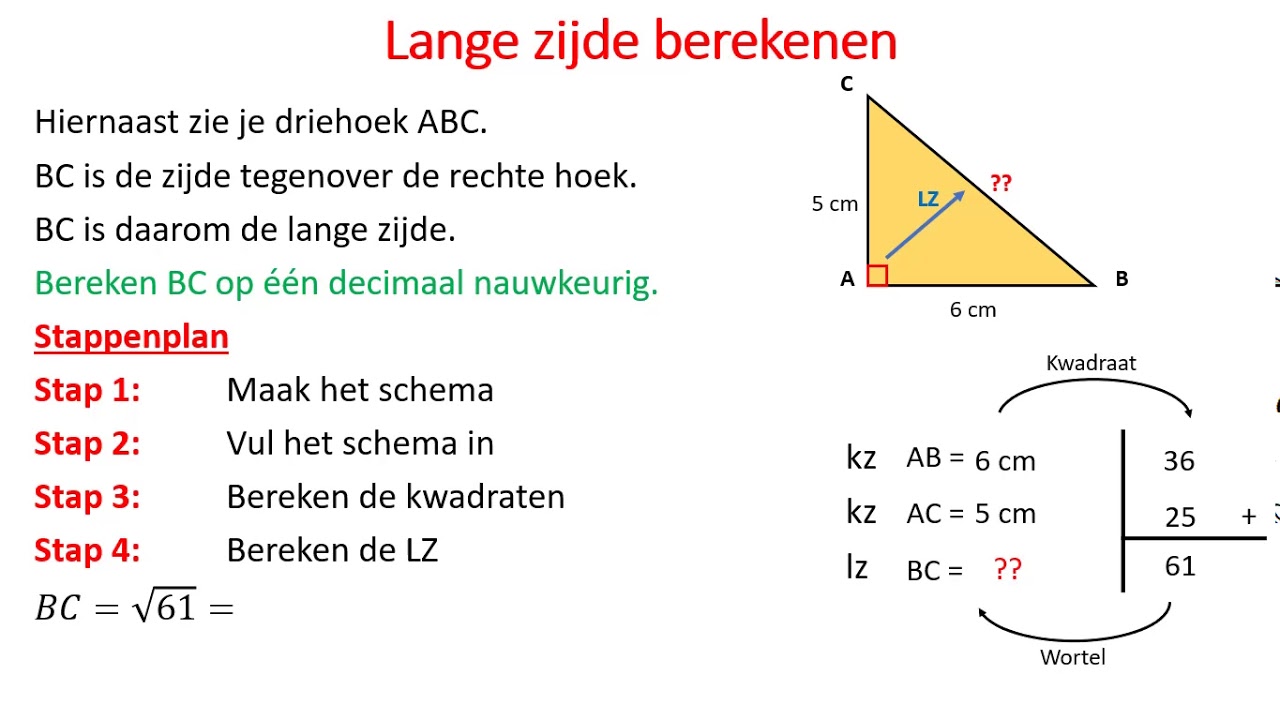
De Stelling van Pythagoras, ontdekt door de Griekse filosoof Pythagoras, stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de schuine zijde (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden (de rechthoekszijden). a² + b² = c².
De sinusregel stelt dat in elke driehoek de verhouding van de lengte van een zijde tot de sinus van de tegenoverliggende hoek constant is. a/sin(A) = b/sin(B) = c/sin(C).
De cosinusregel stelt dat in elke driehoek het kwadraat van de lengte van een zijde gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden, minus tweemaal het product van die lengtes en de cosinus van de ingesloten hoek. c² = a² + b² - 2ab*cos(C).
Voorbeeld: Een rechthoekige driehoek heeft rechthoekszijden van 3 en 4 cm. De schuine zijde is dan sqrt(3² + 4²) = 5 cm.
Voordelen: Nodig voor constructie, navigatie, landmeetkunde, etc. Helpt bij het ontwikkelen van probleemoplossende vaardigheden.
Veelgestelde vragen: Hoe bereken ik de zijde van een rechthoekige driehoek? Met Pythagoras. Wat is de sinusregel? Wat is de cosinusregel? Hoe bereken ik de zijde als ik alleen hoeken ken? Je hebt minstens één zijde nodig.
Tips: Teken altijd een schets van de driehoek. Controleer of je antwoord logisch is.
Conclusie: Het berekenen van de zijde van een driehoek is een fundamentele vaardigheid in de meetkunde met talloze praktische toepassingen. Door de Stelling van Pythagoras, de sinusregel en de cosinusregel te beheersen, kunnen we complexe geometrische problemen oplossen en ons begrip van de wereld om ons heen verdiepen. Blijf oefenen met verschillende voorbeelden en ontdek de fascinerende wereld van de driehoeksmeetkunde. Het begrijpen van driehoeken en hun eigenschappen is niet alleen essentieel voor wiskundige problemen, maar ook voor het oplossen van problemen in de echte wereld, van het ontwerpen van gebouwen tot het navigeren door de sterren. Dus, pak je rekenmachine, teken een driehoek en begin met berekenen!
Perfecte pasvorm brede tennisschoenen voor heren op sandplatz
De nuances van blijkbaar in het frans
Ontdek de bijbel een diepgaande verkenning met uitleg
