Ontdek de geheimen van zijde berekenen: Van driehoek tot piramide!
Hoe bereken je de lengte van een zijde? Deze vraag komt in vele vormen terug in de wiskunde, van eenvoudige driehoeken tot complexe driedimensionale figuren. Het bepalen van een onbekende zijde is een fundamentele vaardigheid in de meetkunde en essentieel voor talloze toepassingen, van architectuur tot engineering. Of je nu een student bent die worstelt met huiswerk of een professional die een snelle opfriscursus nodig heeft, deze gids biedt een uitgebreid overzicht van verschillende methoden om de zijde van een figuur te berekenen.
De zoektocht naar de lengte van een onbekende zijde begint vaak met de stelling van Pythagoras, een eeuwenoude formule die de relatie beschrijft tussen de zijden van een rechthoekige driehoek. Maar de wereld van zijde-berekening strekt zich veel verder uit. Denk aan trigonometrie, die hoeken en zijden verbindt in allerlei driehoeken, of aan de formules voor de oppervlakte en omtrek van verschillende vormen. Het beheersen van deze technieken opent deuren naar een dieper begrip van de geometrie en haar toepassingen in de echte wereld.
Het berekenen van een zijde is niet alleen een abstracte wiskundige oefening; het heeft praktische implicaties in diverse vakgebieden. Stel je voor dat je een architect bent die de optimale afmetingen van een gebouw wil bepalen, of een ingenieur die de lengte van een brugconstructie moet berekenen. In beide gevallen is het nauwkeurig bepalen van de zijdelengtes cruciaal voor het succes van het project. De vaardigheid om een zijde te berekenen is dus niet alleen theoretisch, maar ook praktisch van groot belang.
De geschiedenis van het berekenen van zijden gaat terug tot de oude beschavingen, die geometrie gebruikten voor landmeting, astronomie en bouw. De Babyloniërs en Egyptenaren hadden al kennis van de stelling van Pythagoras, lang voordat Pythagoras zelf werd geboren. Door de eeuwen heen hebben wiskundigen nieuwe methoden en formules ontwikkeld om de zijden van steeds complexere figuren te berekenen, wat heeft bijgedragen aan de vooruitgang van de wetenschap en technologie.
Een veelvoorkomend probleem bij het berekenen van een zijde is het correct identificeren van de relevante gegevens en de juiste formule toepassen. Soms zijn niet alle benodigde gegevens direct beschikbaar en moeten er extra stappen worden ondernomen om ze te vinden. Het is essentieel om de eigenschappen van de betreffende figuur te begrijpen en de juiste methode te kiezen, of het nu de stelling van Pythagoras, trigonometrie of een andere formule is.
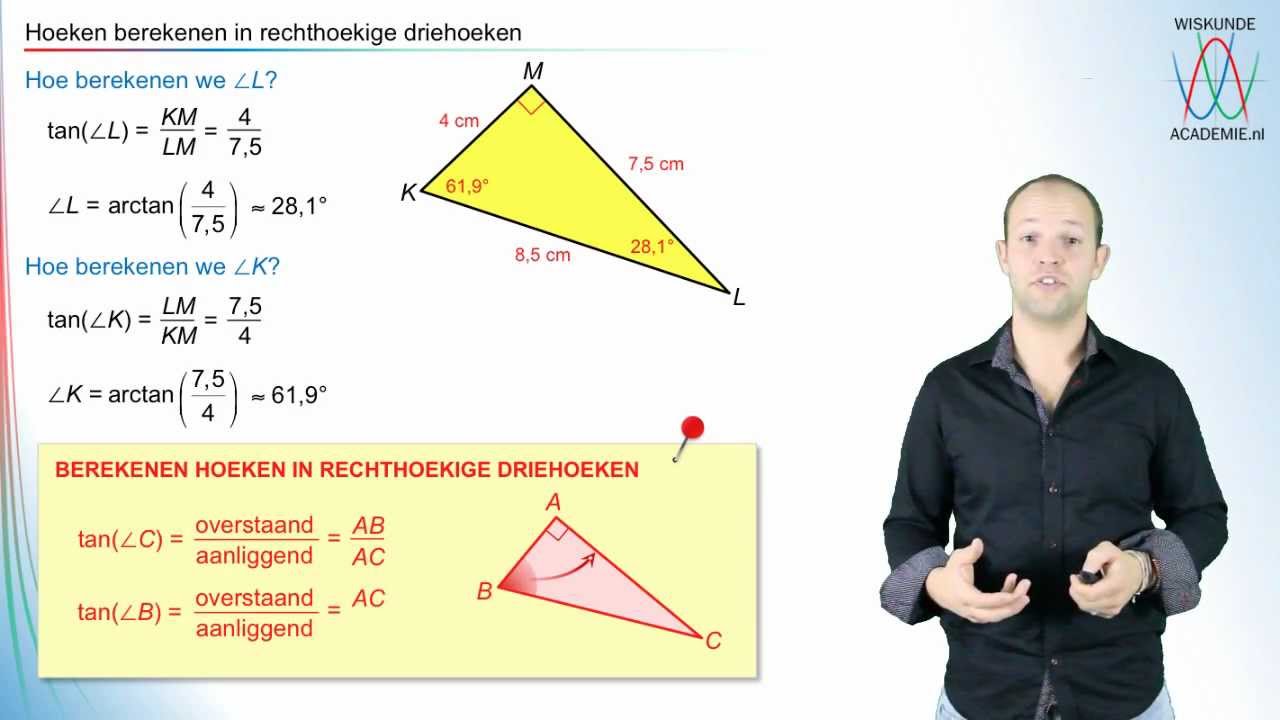
De stelling van Pythagoras stelt dat in een rechthoekige driehoek de som van de kwadraten van de rechthoekszijden gelijk is aan het kwadraat van de schuine zijde (a² + b² = c²). In een driehoek met zijden 3 en 4, is de schuine zijde 5 (3² + 4² = 5²). Met trigonometrie, met behulp van sinus, cosinus en tangens, kunnen zijden en hoeken in elke driehoek worden berekend.
Voordelen van het beheersen van zijde-berekening zijn: 1) Probleemoplossend vermogen verbeteren, 2) Begrip van geometrische principes verdiepen, 3) Toepassing in praktische situaties.
Een actieplan voor het berekenen van een zijde: 1) Identificeer de figuur, 2) Verzamel de bekende gegevens, 3) Kies de juiste formule, 4) Bereken de onbekende zijde.
Veelgestelde vragen: 1) Wat is de stelling van Pythagoras? 2) Hoe gebruik je trigonometrie? 3) Wat is de omtrek van een vierkant? 4) Hoe bereken je de diagonaal van een rechthoek? 5) Wat is de oppervlakte van een cirkel? 6) Hoe bereken je de zijde van een kubus? 7) Wat is de formule voor de oppervlakte van een driehoek? 8) Hoe bereken je de omtrek van een rechthoek?
Tips: Maak een schets van de figuur. Controleer je berekeningen. Gebruik een rekenmachine.
Het berekenen van een zijde is een essentiële vaardigheid in de wiskunde en heeft talloze toepassingen in de praktijk. Van het ontwerpen van gebouwen tot het navigeren met behulp van GPS, de principes van geometrie en zijde-berekening spelen een cruciale rol in onze moderne wereld. Door de verschillende methoden en formules te begrijpen en toe te passen, kunnen we onze probleemoplossende vaardigheden verbeteren en een dieper inzicht krijgen in de wereld om ons heen. Begin vandaag nog met het oefenen en ontdek de fascinerende wereld van geometrie! Door de stelling van Pythagoras, trigonometrie en andere formules te beheersen, open je deuren naar een beter begrip van wiskunde en haar praktische toepassingen. Blijf oefenen en ontdek de vele mogelijkheden die de wereld van geometrie te bieden heeft!
De kracht van padlet ontdek hoe deze online tool samenwerking en creativiteit stimuleert
De grond onder je voeten verliezen wanneer je door je benen zakt
De geheimen van staatsleningen wie investeert erin en waarom
