Conquering Fractions: Your Guide to Addition and Subtraction Mastery
Fractions. Those seemingly simple combinations of numerators and denominators can sometimes feel like a numerical labyrinth. But what if I told you that unlocking the secrets of fraction arithmetic could be less about rote memorization and more about intuitive understanding? This guide will delve into the world of fraction addition and subtraction, offering a fresh perspective on these foundational math concepts.
From slicing a pizza into equal portions to understanding stock market fluctuations, fractions underpin numerous aspects of our daily lives. They represent parts of a whole, allowing us to quantify and manipulate values that fall between whole numbers. Mastering fraction addition and subtraction isn't just about passing math tests; it's about developing a crucial skillset for navigating the world around us.
The concept of fractions dates back to ancient civilizations, with evidence of their use found in Egyptian papyri and Babylonian cuneiform tablets. These early mathematicians recognized the need to represent quantities that were less than a whole unit. Over centuries, the notation and methods for working with fractions evolved, leading to the system we use today.
One of the main challenges learners face with fraction addition and subtraction is the concept of common denominators. Unlike whole number addition, fractions require a shared "unit" before they can be combined. This often involves finding the least common multiple (LCM) of the denominators, a step that can be tricky for some. However, with focused practice, finding common denominators becomes second nature.
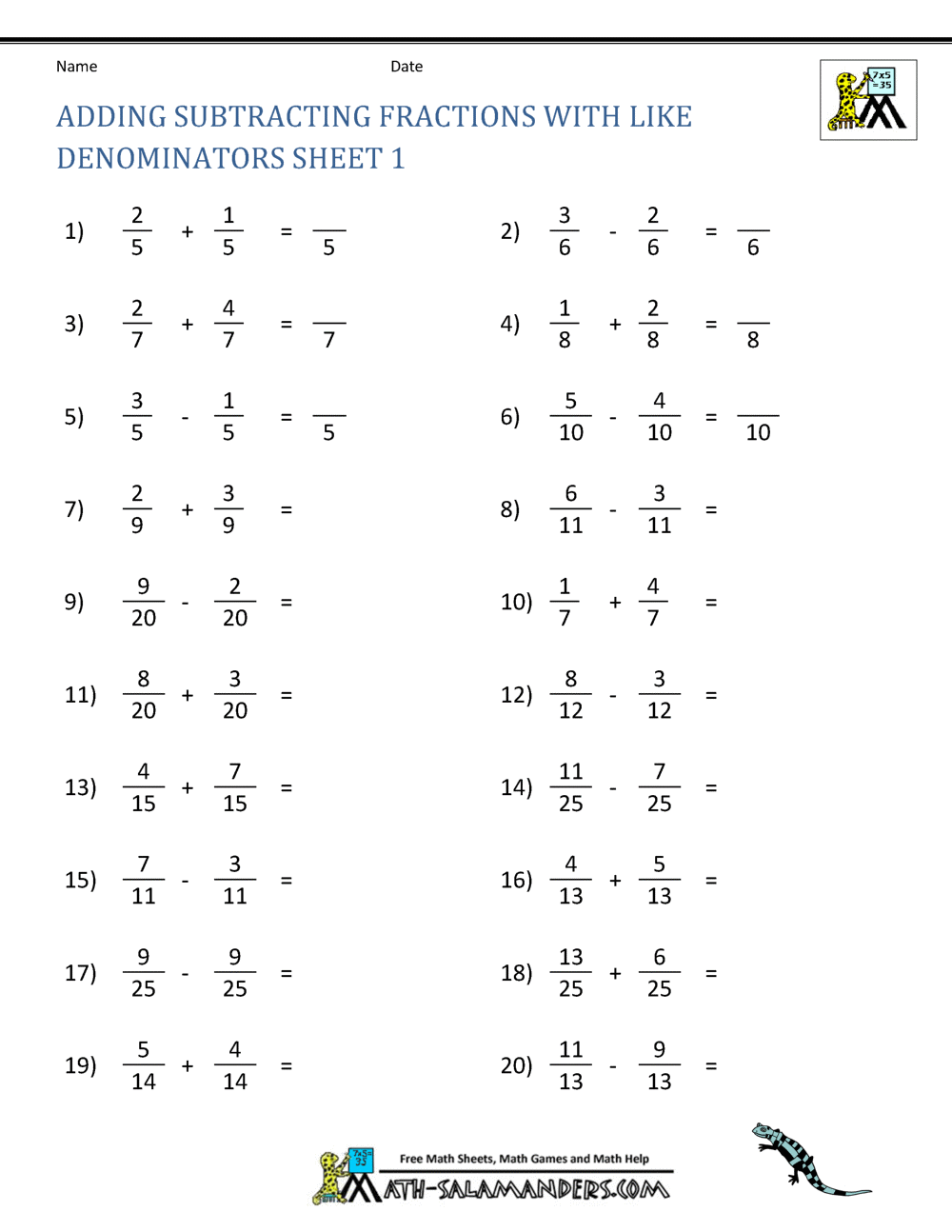
Let's refresh the basics. Adding or subtracting fractions with the same denominator is straightforward. Simply add or subtract the numerators and keep the denominator the same. For example, 1/5 + 2/5 = 3/5. However, when the denominators differ, we must find a common denominator before proceeding. For instance, to add 1/3 and 1/2, we find the least common multiple of 3 and 2, which is 6. We then convert each fraction to have a denominator of 6: 1/3 becomes 2/6, and 1/2 becomes 3/6. Now we can add: 2/6 + 3/6 = 5/6.
Benefit 1: Improved problem-solving skills. Fraction operations enhance logical thinking and reasoning abilities, essential for tackling complex problems in various fields.
Benefit 2: Real-world applicability. From cooking and measuring ingredients to managing finances and understanding discounts, fractions are constantly in use.
Benefit 3: Foundation for advanced math. Mastering fractions is crucial for progressing to algebra, calculus, and other higher-level math concepts.
Action Plan: Start with simple problems involving like denominators. Gradually introduce unlike denominators, focusing on finding common multiples. Practice regularly, using online resources, textbooks, or workbooks.
Checklist: Understand numerator and denominator. Master finding common denominators. Simplify answers to lowest terms.
Step-by-step guide: 1. Identify denominators. 2. If different, find the least common multiple. 3. Convert fractions to equivalent fractions with the common denominator. 4. Add or subtract numerators. 5. Simplify the result.
Recommended resource: Khan Academy
Advantages and Disadvantages of Fraction Addition and Subtraction Practice
| Advantages | Disadvantages |
|---|---|
| Builds foundational math skills | Can be challenging initially |
| Enhances problem-solving abilities | Requires patience and practice |
Best Practices: 1. Visualize with diagrams. 2. Use real-world examples. 3. Break down complex problems. 4. Practice regularly. 5. Seek help when needed.
Real Examples: 1. Sharing a pizza. 2. Measuring ingredients in a recipe. 3. Calculating discounts. 4. Dividing land area. 5. Mixing chemicals in a lab.
Challenges and Solutions: 1. Difficulty finding common denominators: Use prime factorization. 2. Simplifying fractions: Divide by greatest common factor. 3. Mixed numbers: Convert to improper fractions. 4. Negative fractions: Follow integer rules. 5. Word problems: Translate to equations.
FAQ: 1. What is a fraction? 2. How do you add fractions with like denominators? 3. How do you subtract fractions with unlike denominators? 4. What is a mixed number? 5. How do you simplify a fraction? 6. What is the least common multiple? 7. How do fractions apply to real life? 8. Where can I find more practice problems?
Tips and tricks: Use visual aids like pie charts or fraction bars. Practice mental math with simple fractions. Create your own word problems to apply the concepts.
In conclusion, mastering fraction addition and subtraction is a cornerstone of mathematical literacy. From everyday calculations to advanced scientific applications, fractions play a vital role. While the initial learning curve might seem steep, with consistent practice and a focus on understanding the underlying principles, anyone can conquer these essential math concepts. The benefits extend far beyond the classroom, empowering individuals with the skills to solve problems, make informed decisions, and navigate a world filled with fractional quantities. Embrace the challenge, practice diligently, and unlock the power of fractions. Start your journey toward fraction mastery today – it's an investment that will pay dividends throughout your academic and professional life.
Fondo degradado rosa pastel the dreamy design trend you need to know
Unlocking codes potential a journey through vs code setup
Decoding the toyota tacoma 5 lug bolt pattern