Unlocking Electrical Mysteries: Demystifying Current Phasors
Ever feel like electrical circuits are speaking a secret language? Like a cryptic code you just can't crack? Well, honey, let's talk about phasors. Specifically, current phasors. They're the Rosetta Stone for understanding the ebbs and flows of alternating current (AC) circuits, and once you get them, suddenly those oscillating electrons start making a whole lot more sense. Instead of drowning in a sea of sines and cosines, we'll find a sleek, elegant way to represent these wiggly waves.
So, what exactly *is* a current phasor? Imagine a tiny arrow spinning around a clock face. That arrow is a visual representation of the current's magnitude and phase angle. The length of the arrow tells you how much current is flowing, while its position on the clock face tells you where it is in its cycle. Pretty chic, right? By representing AC quantities as these rotating vectors, we can ditch the complicated trigonometry and use simpler algebra to analyze circuits. It's like swapping out a bulky vintage suitcase for a sleek, modern carry-on. You still have all your essentials, but it's just so much easier to manage.
Historically, grappling with AC circuit analysis was a major headache. Before phasor representation, engineers had to wrestle with differential equations, which, let's be honest, can be a total buzzkill. Then along came Charles Proteus Steinmetz, a total electrical genius, who pioneered the use of phasors, revolutionizing circuit analysis and basically making everyone's life a whole lot easier. Talk about a game-changer. His insights transformed a complex, time-consuming process into something much more manageable.
Calculating the phasor for the current is crucial for understanding how AC circuits behave. It allows us to analyze complex circuits with multiple components, predict voltage drops and currents, and design systems that operate efficiently. Without phasor analysis, designing anything from a simple toaster to a complex power grid would be a nightmare. Imagine trying to navigate a city without a map – total chaos. Similarly, phasors provide the roadmap for navigating the complexities of AC circuits.
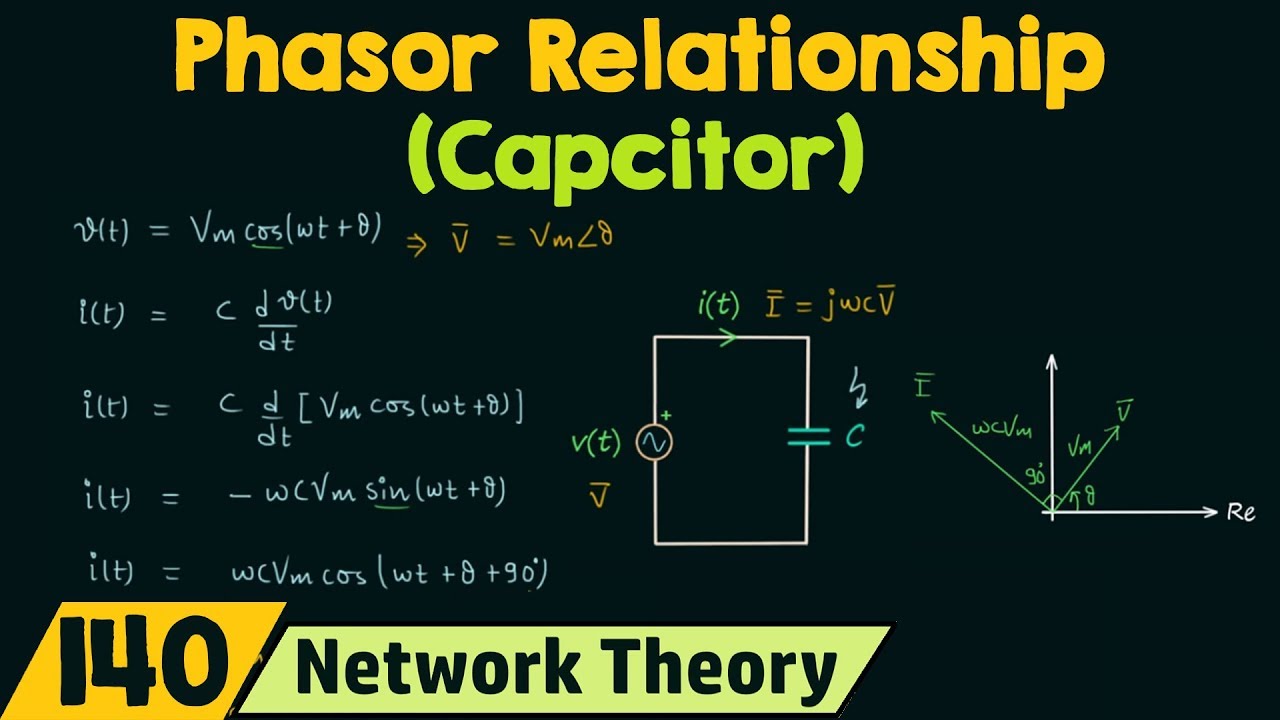
Essentially, finding the phasor representation of the current involves converting the sinusoidal current waveform into a complex number. This complex number has a magnitude corresponding to the peak value of the current and an angle representing the phase shift. So, if you're given a current represented by i(t) = Imcos(ωt + θ), its phasor equivalent is I = Im∠θ. This compact notation encapsulates all the essential information about the current's magnitude and phase, making circuit calculations much smoother. Think of it as the ultimate summary—all the key details without any of the fluff.
One benefit of using phasors is simplification of complex calculations. With phasors, we can use simple algebraic operations like addition and subtraction to analyze circuits, instead of struggling with trigonometric identities. A second advantage is visualization. Phasor diagrams provide a clear visual representation of the relationship between voltage and current in a circuit. Finally, phasors make it easier to understand concepts like impedance and power factor, which are crucial for optimizing circuit performance.
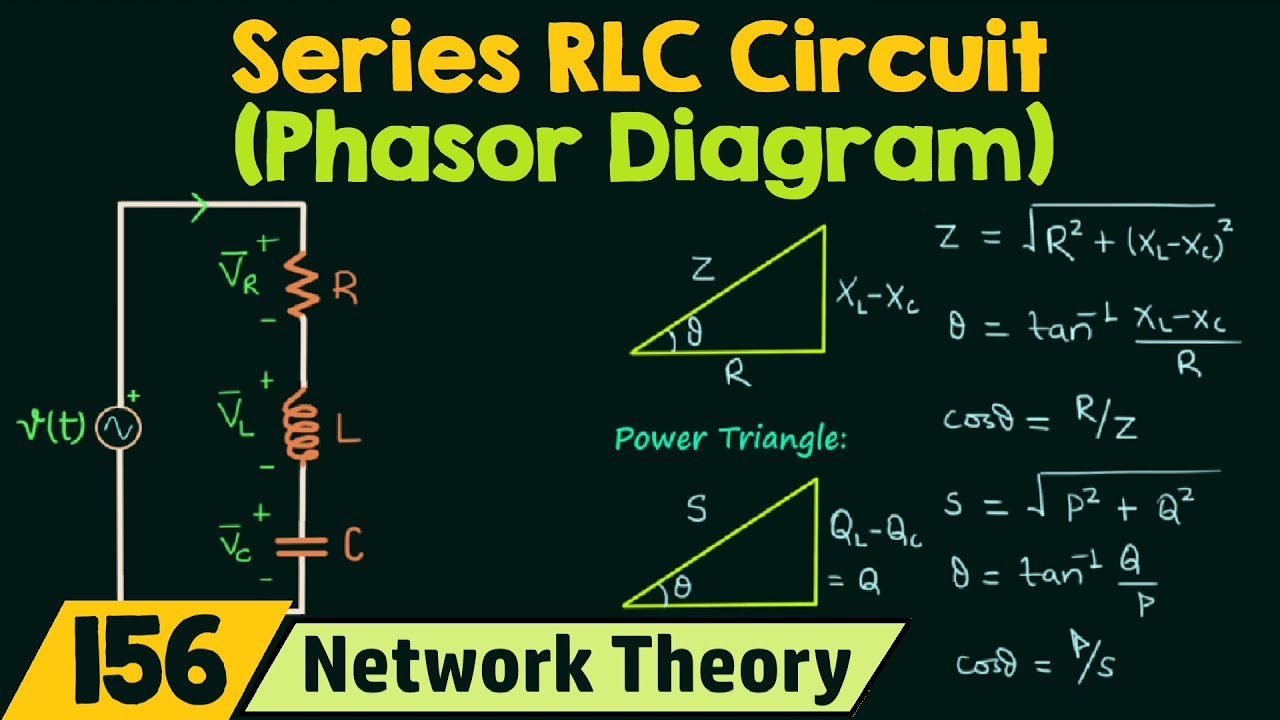
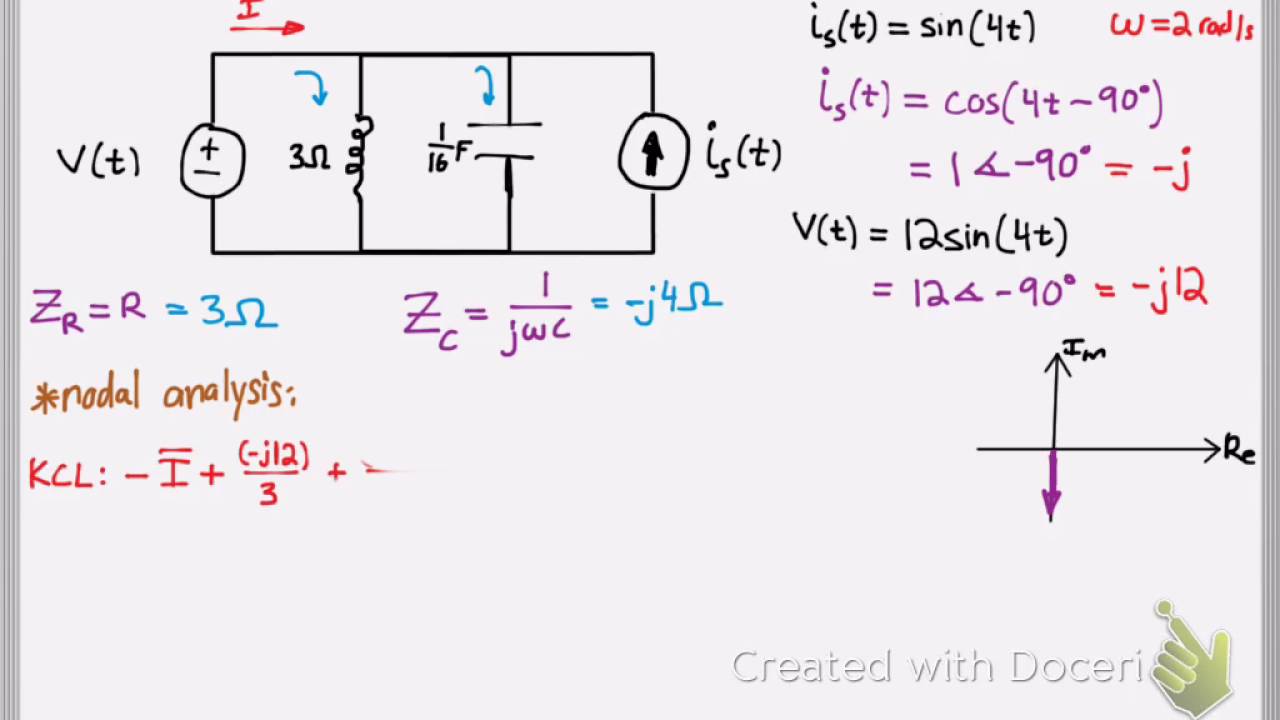
Let's look at a simple example. Imagine a circuit with a resistor and an inductor. To find the current phasor, we first need to find the impedance of the circuit. Then, we divide the voltage phasor by the impedance to get the current phasor.
Advantages and Disadvantages of Using Phasors
| Advantages | Disadvantages |
|---|---|
| Simplifies complex calculations | Primarily applicable to sinusoidal waveforms |
| Provides a clear visual representation | Can be initially challenging to grasp |
| Facilitates understanding of impedance and power factor | Doesn't directly represent transient behavior |
To determine a current phasor, follow these steps: 1) Identify the amplitude and phase angle of the sinusoidal current. 2) Convert the sinusoidal expression into its phasor equivalent using complex number representation.
FAQs: What is a phasor? How do you find the phasor for the current? What are the benefits of using phasors? What is the difference between a phasor and a vector? What is impedance? What is the power factor? How do you calculate the impedance of a circuit? How are phasors used in AC circuit analysis?
Tips and tricks for working with phasors: always remember to convert your sinusoidal functions to the same frequency before performing operations with phasors. Make sure to use the correct units for your calculations. Practicing with different circuit examples will help you solidify your understanding of phasor analysis.
In conclusion, mastering current phasors is essential for anyone working with AC circuits. They provide an elegant and efficient way to analyze complex circuits, making it easier to understand and design electrical systems. By transforming confusing sinusoidal waveforms into manageable vectors, phasors unlock a world of possibilities in electrical engineering. From designing simple circuits to complex power grids, phasor analysis is an indispensable tool. So, embrace the power of phasors, and let them illuminate your understanding of the electrifying world of AC circuits. Don't just admire the sparkle, understand the current that makes it shine. Dive into the world of phasors and unlock a deeper appreciation for the magic of electricity. Start exploring, practicing, and you’ll soon find yourself navigating the complex world of AC circuits with confidence and flair.
The twisted tragedy exploring the fnaf william afton and michael relationship
The allure of the lunar rock rav4 hybrid a confluence of style and sustainability
The haunting pull of home exploring the lyrics of caledonia
