Unlocking Electrical Mysteries: Mastering Phasor Voltage Calculations
Ever felt lost in a maze of sinusoidal waves and complex numbers when dealing with AC circuits? The secret to navigating this intricate electrical landscape lies in understanding phasor voltages. Phasor voltage calculations are a fundamental tool for analyzing AC circuits, simplifying complex sinusoidal functions into manageable vector representations.
Imagine trying to analyze a circuit with multiple AC sources operating at different frequencies and phase shifts. Using traditional time-domain analysis can quickly become overwhelming. Phasors provide an elegant shortcut, transforming intricate trigonometric equations into simpler algebraic operations in the frequency domain. This simplification unlocks the ability to analyze complex circuits with ease and precision.
Determining phasor voltage is crucial for electrical engineers and anyone working with AC circuits. It’s the foundation for understanding power flow, impedance matching, and resonance. From designing efficient power systems to developing cutting-edge electronics, phasor analysis plays a vital role. Without a solid grasp of phasor voltage, unraveling the complexities of AC circuits becomes an insurmountable challenge.
Historically, the concept of phasors emerged with the development of AC power systems in the late 19th century. Charles Proteus Steinmetz, a pioneering electrical engineer, is credited with popularizing the use of phasors for simplifying AC circuit analysis. His work laid the groundwork for modern power system analysis and design. The key issue addressed by phasor calculations is the complexity of dealing with sinusoidal functions in AC circuits. Phasors convert these functions into simpler vector representations, making calculations significantly easier.
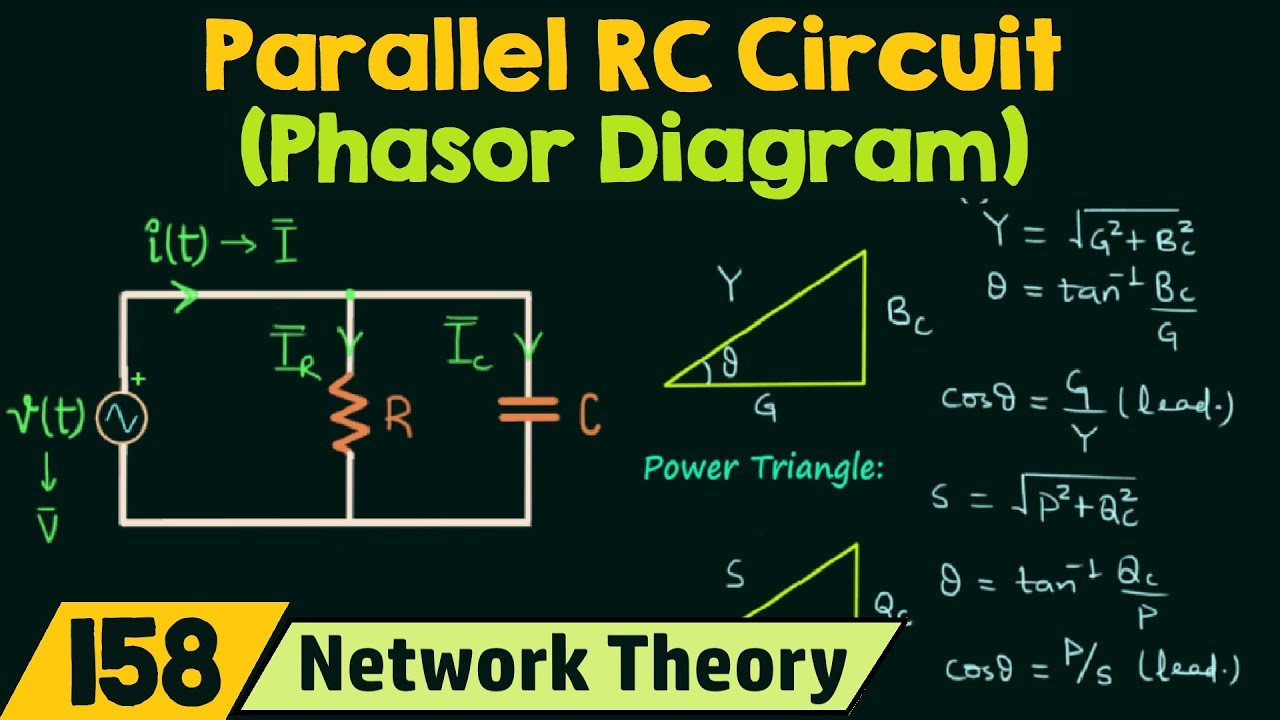
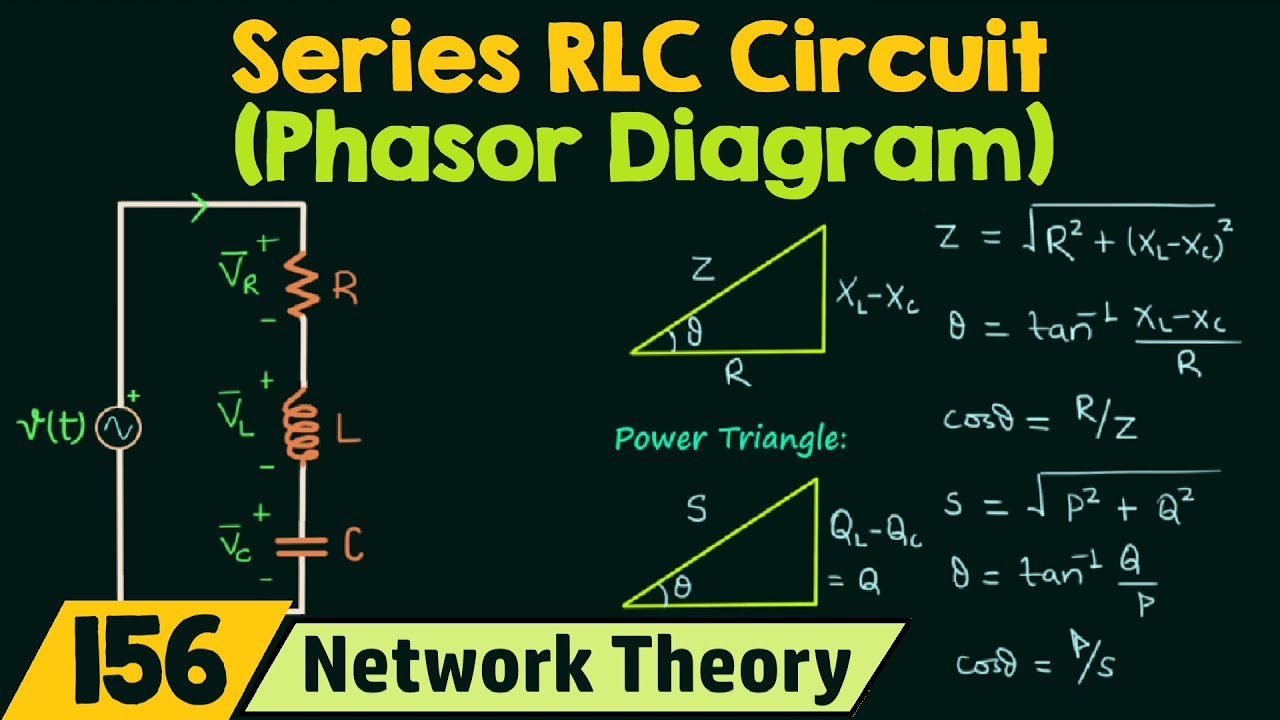
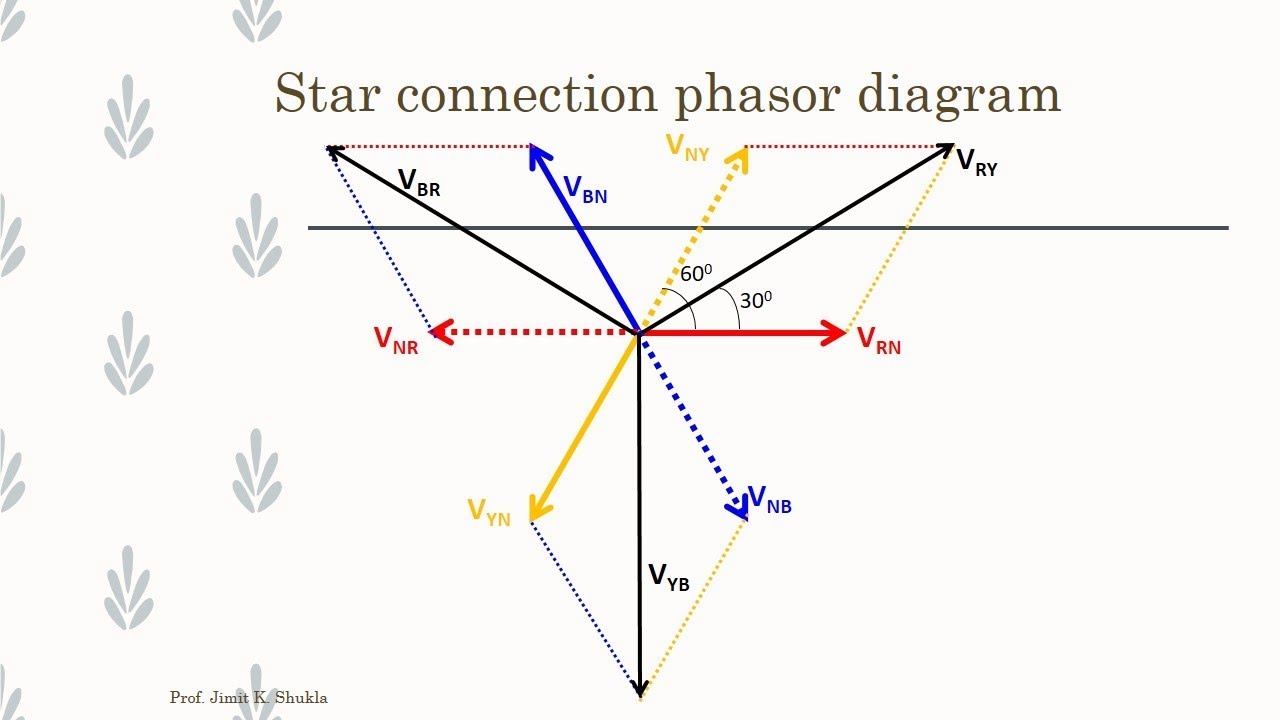
So, what exactly is a phasor? A phasor is a complex number representing the magnitude and phase angle of a sinusoidal function. It simplifies the representation of a sinusoidal voltage or current, allowing us to perform calculations using complex algebra instead of trigonometry. A phasor voltage, therefore, represents the voltage of an AC source as a rotating vector in the complex plane. Its magnitude corresponds to the peak voltage, and its angle represents the phase shift relative to a reference.
Understanding how to determine phasor voltage offers several advantages. It simplifies AC circuit analysis, enables efficient power system design, and is essential for designing and analyzing electronic circuits. By converting time-domain functions into phasors, we can apply algebraic techniques to solve complex AC circuit problems, significantly reducing the computational burden. For instance, adding two sinusoidal voltages with different phases becomes a straightforward vector addition in the phasor domain.
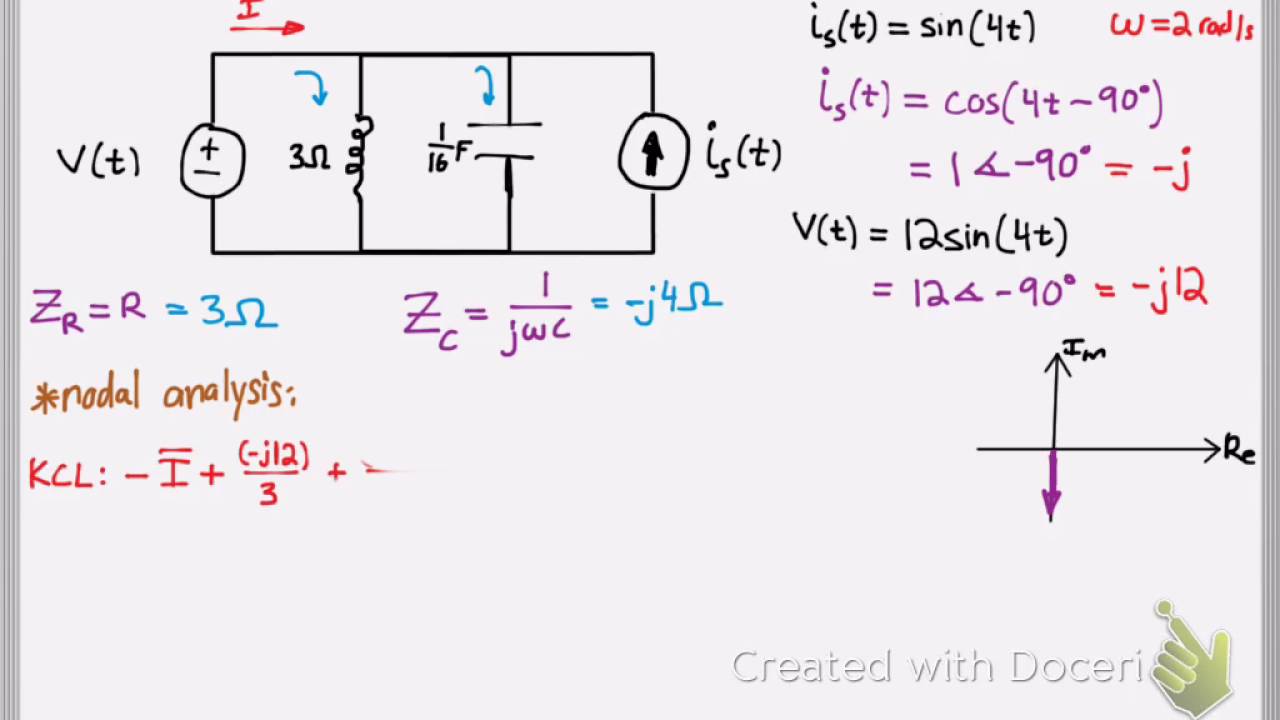
To calculate the phasor voltage, you need the peak voltage (Vp) and the phase angle (θ). The phasor voltage (V) can be expressed in polar form as V = Vp∠θ or in rectangular form as V = Vp(cos θ + j sin θ). For example, a sinusoidal voltage described by v(t) = 170sin(ωt + 30°) has a phasor representation of V = 170∠30°.
A step-by-step guide to determining phasor voltage: 1) Identify the peak voltage and phase angle of the sinusoidal voltage. 2) Represent the phasor voltage in either polar or rectangular form. 3) Use the phasor representation to perform circuit analysis calculations.
Advantages and Disadvantages of Phasor Calculations
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit analysis | Applies only to steady-state sinusoidal signals |
| Facilitates complex circuit analysis | Requires understanding of complex numbers |
| Enables efficient power system design | Does not capture transient behavior |
Best Practices for Phasor Calculations: 1) Always ensure all sinusoidal functions are at the same frequency. 2) Clearly define the reference phase. 3) Use appropriate units for voltage and angle. 4) Double-check calculations for accuracy. 5) Use software tools for complex circuit analysis.
Real World Examples: Phasor calculations are used in power system analysis, motor control, filter design, and communication systems.
Challenges and Solutions: A common challenge is dealing with non-sinusoidal waveforms. Fourier analysis can be used to decompose these waveforms into sinusoidal components, which can then be analyzed using phasors.
FAQ: What is a phasor? How is it different from a vector? Why are phasors important? What are the applications of phasor analysis? How do I convert between polar and rectangular forms? What is impedance in the phasor domain? What are the limitations of phasor analysis? How can I improve my understanding of phasors?
Tips and Tricks: Familiarize yourself with complex number operations. Practice converting between time-domain and phasor representations. Use software tools for visualization and calculations.
In conclusion, understanding how to calculate phasor voltage is essential for anyone working with AC circuits. This powerful technique simplifies complex circuit analysis, enabling efficient design and analysis of electrical systems. Mastering phasor calculations empowers you to navigate the world of AC circuits with confidence, from basic circuit analysis to advanced power system design. By embracing this crucial tool, you unlock the ability to solve complex electrical problems and push the boundaries of technological innovation. Explore the resources available, practice diligently, and you'll find that the complexities of AC circuits become manageable, opening a world of possibilities in electrical engineering and beyond. Take the time to master this crucial skill – it will be a valuable asset in your electrical engineering journey.
Unlocking the baking code your guide to a metric conversion chart for grams to cups
Cromarty green the enchanting hue by farrow and ball
The rise of dark fantasy villainy