Unlocking the Secrets of 50: A Deep Dive into its Divisors
Ever wondered what makes a number tick? What hidden structures lie beneath its surface? Today, we're cracking the code of 50, exploring the fascinating world of its divisors. What are the factors of 50? This seemingly simple question opens a door to a universe of mathematical concepts.
Understanding the divisors of a number is fundamental to many areas of math. From basic arithmetic to advanced number theory, the factors of 50, or any number for that matter, play a crucial role. They help us understand relationships between numbers, simplify fractions, and even solve complex equations. Think of them as the building blocks of a number's identity.
So, what exactly are the divisors of 50? Simply put, they are the numbers that divide 50 evenly without leaving a remainder. They are the integers that can be multiplied by another integer to result in 50. This concept, though seemingly straightforward, has a rich history and a surprising number of applications.
The concept of divisors, or factors, dates back to ancient civilizations. From the Babylonians to the Greeks, mathematicians have been fascinated by the relationships between numbers and their divisors. This exploration led to the development of fundamental concepts like prime numbers, composite numbers, and the very idea of divisibility. Understanding these principles laid the groundwork for much of modern mathematics.
The importance of knowing the divisors of 50, or any number, extends beyond theoretical mathematics. It has practical applications in fields like computer science, cryptography, and even music theory. For example, in computer programming, understanding factors can help optimize algorithms and data structures. In cryptography, the concept of prime factorization is essential for securing information.
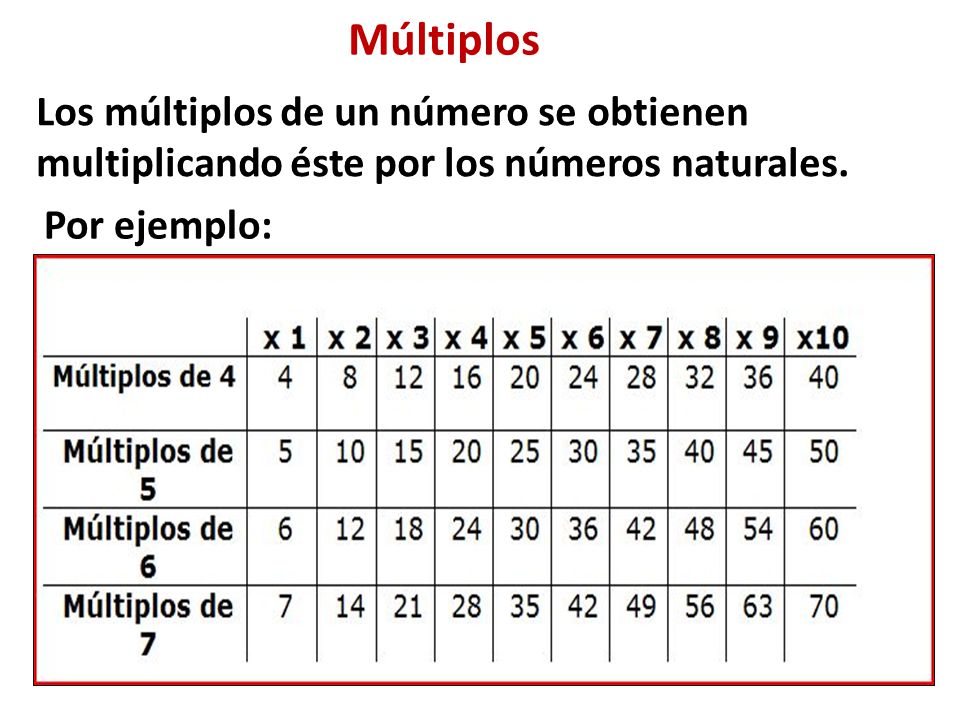
The divisors of 50 are 1, 2, 5, 10, 25, and 50. Each of these numbers divides 50 without leaving a remainder. For example, 50 divided by 2 is 25, and 50 divided by 5 is 10.
One benefit of knowing the factors of a number is in simplifying fractions. For example, if you have the fraction 50/100, knowing that 50 is a divisor of 100 allows you to simplify it to 1/2. This makes calculations easier and more efficient.
Another benefit is in finding the greatest common divisor (GCD) and least common multiple (LCM) of two numbers, which are crucial concepts in various mathematical operations.
A third benefit is in understanding prime factorization, a cornerstone of number theory and cryptography. By breaking down a number into its prime factors, we can gain deeper insights into its properties and relationships with other numbers.
To find the divisors of a number like 50, start by dividing it by 1. Then, check for divisibility by 2, 3, 4, and so on, until you reach half of the number. List each number that divides evenly. Finally, include the number itself.
Advantages and Disadvantages of Working with Divisors
While there are no inherent disadvantages to understanding divisors, the process of finding them for very large numbers can be computationally intensive.
Finding divisors can be a valuable educational exercise for students learning about number theory and basic arithmetic. It helps develop problem-solving skills and reinforces fundamental mathematical concepts.
Frequently Asked Questions:
1. What is a divisor? A divisor is a number that divides another number evenly.
2. What are the factors of 50? The factors of 50 are 1, 2, 5, 10, 25, and 50.
3. Why are divisors important? They are fundamental to understanding number relationships and have applications in various fields.
4. How do I find the divisors of a number? Systematically check for divisibility by numbers starting from 1.
5. What is the difference between a divisor and a factor? They are essentially the same thing.
6. What is the greatest common divisor? The largest number that divides two or more numbers evenly.
7. What is the least common multiple? The smallest number that is a multiple of two or more numbers.
8. How are divisors used in real life? They are used in various fields, from computer programming to cryptography.
In conclusion, understanding the divisors of a number like 50 is a fundamental concept in mathematics. While seemingly simple, it unlocks a deeper understanding of number relationships, with applications spanning diverse fields. From simplifying fractions to exploring the foundations of number theory, the factors of 50 provide a valuable entry point into the fascinating world of numbers. Take the time to explore the divisors of other numbers, and discover the hidden patterns and connections that await. By understanding the building blocks of numbers, we gain a deeper appreciation for the elegant structure of mathematics itself. This knowledge empowers us to solve problems, create efficient algorithms, and appreciate the intricate beauty of the numerical world around us. So, keep exploring, keep questioning, and keep unlocking the secrets of numbers!
Timeless elegance linen dresses for women over 60
Crystal clear vision mastering rav4 windshield wiper replacement
Edible elegance elevate your cakes with flower molds
