Unraveling the Enigma: Undefined Terms in Geometry Examples
Have you ever wondered how mathematicians build complex geometric systems? It all starts with a few fundamental building blocks that are, surprisingly, left undefined. These "undefined terms in geometry" might sound paradoxical, but they're the bedrock upon which our understanding of shapes, lines, and spaces rests. Intrigued? Let's delve into this fascinating world and explore the crucial role these undefined terms play.
Imagine trying to describe a house without using the words "wall," "door," or "roof." It seems impossible, right? Yet, that's precisely what geometry does with its undefined terms. It's like agreeing on a secret language where everyone understands the meaning without needing a dictionary. These terms, while lacking formal definitions, are imbued with intuitive understanding. They form the foundation of geometric axioms and postulates, the self-evident truths from which all other geometric concepts are logically derived.
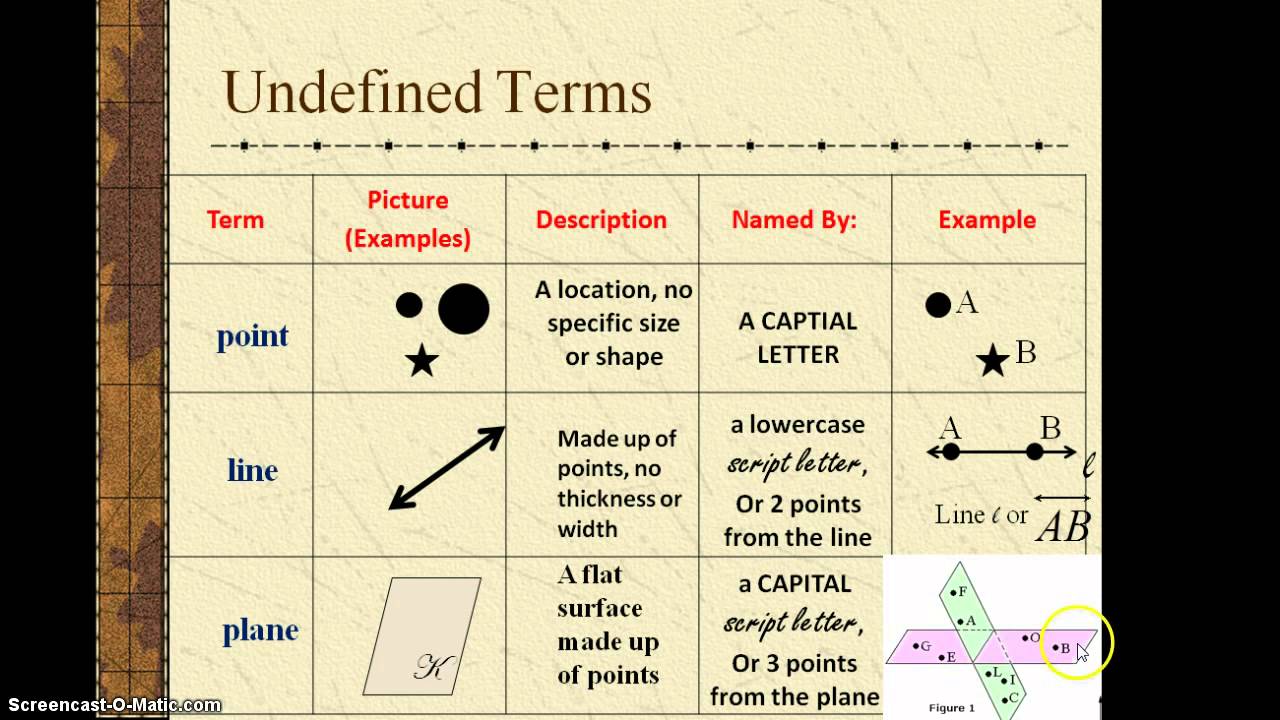
The history of undefined terms in geometry takes us back to ancient Greece, with Euclid's groundbreaking work, "Elements." Euclid recognized the need for a starting point, for fundamental concepts that were so basic, they could only be grasped intuitively. He introduced the ideas of a "point," a "line," and a "plane" as his undefined terms, laying the groundwork for a system of geometry that has endured for millennia. Think of it as building a grand structure - you need a solid foundation to support everything else.
But why are these terms left undefined? Wouldn't it be easier to have concrete definitions? Not really. Defining something means relating it to something else, which would then require its definition and so on, leading to a never-ending loop. The undefined terms act as the starting point, the bedrock, preventing this infinite regression. They provide a common ground, a shared understanding from which we can build upon. It's like the rules of a game – everyone agrees on them upfront so the game can be played.
Let's consider some examples. A "point" in geometry isn't a dot on a paper, but an abstract idea representing a location in space. It has no size, only position. Similarly, a "line" isn't just a straight mark; it's an infinite set of points extending endlessly in both directions. A "plane" is a flat, two-dimensional surface that extends infinitely in all directions. These simple yet powerful concepts, while undefined, are the building blocks for understanding more complex geometric figures like triangles, circles, and cubes.
The elegance of geometry lies in its ability to construct a vast and intricate world from these undefined terms. By using logic and reasoning, we can define other geometric terms and prove theorems. It's like creating a complex tapestry using only a few basic threads. The undefined terms are the starting point, the inspiration, and the foundation of geometric thought.
So, the next time you encounter geometry, remember the undefined terms. They might seem mysterious at first, but they're the unsung heroes, the silent architects, shaping our understanding of the world around us. They remind us that even in the seemingly complex world of mathematics, sometimes, the most powerful concepts are those we intuitively grasp but can't quite define.
Dive into digital expression the versatility of emoji
Inked with iron decoding the intrigue of mike tyson tattoo ideas
Sherwin williams paint colors on houses inspiration
